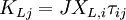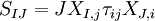Piola-Kirchhoff stress tensor

In the case of finite deformations, the Piola-Kirchhoff stress tensors are used to express the stress relative to the reference configuration. This is in contrast to the Cauchy stress tensor which expresses the stress relative to the present configuration. For infinitesimal deformations or rotations, the Cauchy and Piola-Kirchoff tensors are identical. These tensors take their names from Gabrio Piola and Gustav Kirchhoff.

Additional recommended knowledge

Better weighing performance in 6 easy steps

Correct Test Weight Handling Guide: 12 Practical Tips

Daily Sensitivity Test

1^st Piola-Kirchhoff stress tensor

Whereas the Cauchy stress tensor, τ_ij, relates forces in the present configuration to areas in the present configuration, the 1^st Piola-Kirchhoff stress tensor, K_Lj relates forces in the present configuration with areas in the reference ("material") configuration. K_Lj is given by

where J is the Jacobian, and X_L,i is the inverse of the deformation gradient.

Because it relates different coordinate systems, the 1^st Piola-Kirchhoff stress is a two-point tensor. In general, it is not symmetric. The 1^st Piola-Kirchhoff stress is the 3D generalization of the 1D concept of engineering stress.

If the material rotates without a change in stress state (rigid rotation), the components of the 1^st Piola-Kirchhoff stress tensor will vary with material orientation.

The 1^st Piola-Kirchhoff stress is energy conjugate to the deformation gradient.

2^nd Piola-Kirchhoff stress tensor

Whereas the 1^st Piola-Kirchhoff stress relates forces in the current configuration to areas in the reference configuration, the 2^nd Piola-Kirchhoff stress tensor S_IJ relates forces in the reference configuration to areas in the reference configuration. The force in the reference configuration is obtained via a mapping that preserves the relative relationship between the force direction and the area normal in the current configuration.

This tensor is symmetric.

If the material rotates without a change in stress state (rigid rotation), the components of the 2^nd Piola-Kirchhoff stress tensor will remain constant, irrespective of material orientation.

The 2^nd Piola-Kirchhoff stress tensor is energy conjugate to the Green-Lagrange strain.

References

Introduction to the mechanics of a continuum medium, L. E. Malvern, Prentice-Hall, Englewood Cliffs, NJ, 1969.