To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Simple shear
Product highlightSimple shear is a special case of deformation of a fluid where only one component of velocity vectors has a non-zero value: Vx = f(x,y) Vy = Vz = 0 And the gradient of velocity is perpendicular to it:
where
The deformation gradient tensor Γ for this deformation has only one non-zero term:
Simple shear with the rate
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Simple_shear". A list of authors is available in Wikipedia. |





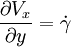 ,
,
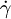 is the
is the 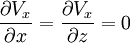
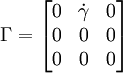
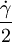 and rotation with the rate of
and rotation with the rate of