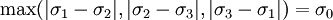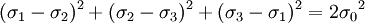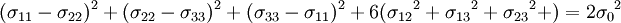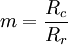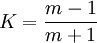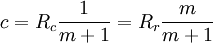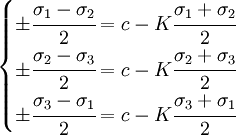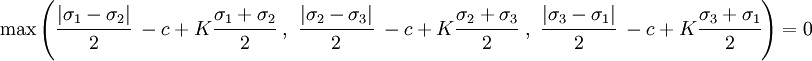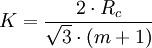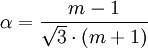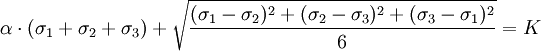My watch list

Yield surface

Yield surface is described in three dimensional space of stresses, and encompasses the elastic region of material behavior. The states of stress of material inside the yield surface are elastic, when the stress reaches this surface it reaches the yield point. Then the material behaviour becomes plastic, because the stress cannot cross this surface.

Useful means of describing yield surface include expressing it in the terms of principal stresses ( $σ 1,σ 2,σ 3$ ), or using stress invariants ( $I 1, I 2, I 3$ ).

There are several different yield surfaces known in engineering, and those most popular are listed below.

Additional recommended knowledge

How to ensure accurate weighing results every day?

How to quickly check pipettes?

Weighing the right way

1 List of symbols used in this article
2 Tresca - Guest yield surface
3 Huber - Mises - Hencky, also known as Prandtl - Reuss yield surface
4 Mohr - Coulomb yield surface
5 Drucker - Prager yield surface
6 Brestler - Pister criterion
7 Willam - Warnke criterion
8 See also

List of symbols used in this article

Following symbols are used below:

σ 1

- principal stress in direction along first axis

σ 2

- principal stress in direction along second axis

σ 3

- principal stress in direction along third axis

σ 0

- yield stress for single parametric yield surface

R c

- yield strength during compression

R r

- yield strength during tension

m

- ratio of yield strengths

c

- material cohesion

α

- stress coefficient

K

- material stiffness for two parametric yield surface (

R c, R r

)

Tresca - Guest yield surface

This is the most simple yield surface, and it is taken to be the work of Henri Tresca. It is also referred as the TG criterion. In terms of the principal stresses it is expressed as

${\max(|\sigma_1 - \sigma_2| , |\sigma_2 - \sigma_3| , |\sigma_3 - \sigma_1| ) = \sigma_0 }\!$

Figure 1 shows the TG criterion in the three dimensional space of principal stresses. It is a prism of six sides and having infinite length. This means that the material remains elastic when all three principal stresses are roughly equivalent (a hydrostatic pressure), no matter how much it is compressed or stretched. However, when the material is subject to shearing and one of principal stresses becomes smaller (or larger) than the others, then the yield surface is reached and material enters the plastic domain.

Figure 2 shows the Tresca-Guest criterion in two dimensional space, it is a cross section of the prism along the $σ 1,σ 2$ plane.

Huber - Mises - Hencky, also known as Prandtl - Reuss yield surface

This is another simple yield surface, which perhaps explains why it is credited to so many authors. Who is the real author depends on the university, although often it is credited to Maximilian Huber and Richard von Mises (see von Mises stress). It is also referred to as the HMH criterion. It is expressed in the principal stresses as

${(\sigma_1 - \sigma_2)^2 + (\sigma_2 - \sigma_3)^2 + (\sigma_3 - \sigma_1)^2 = 2 {\sigma_0}^2 }\!$

In the non-principal stresses, it takes the form of

$(\sigma_{11} - \sigma_{22})^2 + (\sigma_{22} - \sigma_{33})^2 + (\sigma_{33} - \sigma_{11})^2 + 6 ({\sigma_{12}}^2 + {\sigma_{13}}^2 + {\sigma_{23}}^2 + ) = 2 {\sigma_0}^2$

Figure 3 shows the HMH criterion in the three dimensional space of principal stresses. It is a circular cylinder of infinite length, with the same angle to all three axes.

Figure 4 shows the Huber-Mises-Hencky criterion in two dimensional space compared with Tresca-Guest criterion. HMH is a cross section of this cylinder on the plane of $σ 1,σ 2$ , which produces an ellipse.

Mohr - Coulomb yield surface

It is a first two-parametric yield surface, the parameters are $R c$ and $R r$ which are the maximum values for compression and tension for given material. This model is often used to model concrete, soil or granular materials. This model is the first one that takes shearing into account. It is expressaed as follows:

$m = \frac {R_c}{R_r}$

$K = \frac {m-1}{m+1}$

$c = {R_c} \frac {1}{m+1} = {R_r} \frac {m}{m+1}$

$\left\{{\begin{matrix} \pm\cfrac{\sigma_1 - \sigma_2}{2} = c - K \cfrac{\sigma_1 + \sigma_2}{2} \\ \pm\cfrac{\sigma_2 - \sigma_3}{2} = c - K \cfrac{\sigma_2 + \sigma_3}{2} \\ \pm\cfrac{\sigma_3 - \sigma_1}{2} = c - K \cfrac{\sigma_3 + \sigma_1}{2} \end{matrix}}\right.$

To plot this surface on Fig. 5 the following formula was used:

$\max\left(\cfrac{|\sigma_1 - \sigma_2|}{2}\ - c + K \cfrac{\sigma_1 + \sigma_2}{2}\ ,\ \cfrac{|\sigma_2 - \sigma_3|}{2}\ - c + K \cfrac{\sigma_2 + \sigma_3}{2}\ ,\ \cfrac{|\sigma_3 - \sigma_1|}{2}\ - c + K \cfrac{\sigma_3 + \sigma_1}{2} \right) = 0$

Figure 5 shows Mohr-Coulomb criterion in three dimensional space of principal stresses. It is a conical prism. If $K = 0$ then it becomes Tresca-Guest criterion, thus $K$ determines the inclination angle of conical surface.

Figure 6 shows Mohr-Coulomb criterion in two dimensional space, it is a cross section of this conical prism on the plane of $σ 1,σ 2$ , which produces a shape shown below.

Drucker - Prager yield surface

This criterion is most often used for concrete, both normal and shear stresses are taken into account.

$m = \frac {R_c}{R_r}$

$K = \frac {2 \cdot R_c}{\sqrt{3}\cdot(m+1)}$

$\alpha = \frac {m-1}{\sqrt{3}\cdot(m+1)}$

$\alpha \cdot \left( \sigma_1 + \sigma_2 + \sigma_3 \right) + \sqrt{\frac{(\sigma_1 - \sigma_2)^2 + (\sigma_2 - \sigma_3)^2 + (\sigma_3 - \sigma_1)^2}{6}} = K$

Figure 7 shows Drucker-Prager criterion in three dimensional space of principal stresses. It is a regular cone.

Figure 8 shows Drucker-Prager criterion in two dimensional space, it is a cross section of this cone on the plane of $σ 1,σ 2$ , which produces an ellipsioidal shape. It is compared here with Mohr-Colulomb criterion.

Brestler - Pister criterion

This criterion is a first criterion that uses three parameters. It is similar to HMH criterion but additional parameter affects the cylinder radius using an $x 2$ function. Thus cylinder's section along its axis is no longer a rectangle (or rather two parallel lines, since the cylinder has infinite length) but a parabola.

Willam - Warnke criterion

This is the most advanced yield surface, it takes the idea from Brestler - Pister a bit further and applies it to Mohr-Colulomb criterion. The resulting surface is smooth (unlike Mohr-Colulumb) and has first and second derivative fully defined on every point of its surface which is an important property. This smoothness allows optimisations during calculations when searching for a yield point on the surface (using gradient method for instance).