To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Strain (materials science)
In any branch of science dealing with materials and their behaviour, strain is the geometrical expression of deformation caused by the action of stress on a physical body. Strain is calculated by first assuming a change between two body states: the beginning state and the final state. Then the difference in placement of two points in this body in those two states expresses the numerical value of strain. Strain therefore expresses itself as a change in size and/or shape. If strain is equal over all parts of a body, it is referred to as homogeneous strain; otherwise, it is inhomogeneous strain. In its most general form, the strain is a symmetric tensor. Product highlight
Quantifying strainGiven that strain results in the deformation of a body, it can be measured by calculating the change in length of a line or by the change in angle between two lines (where these lines are theoretical constructs within the deformed body). The change in length of a line is termed the stretch, absolute strain, or extension, and may be written as where
The extension ( Strain is a dimensionless quantity. It has no units of measure because in the formula the units of length "cancel out". Strain is often expressed in dimensions of metres/metre or inches/inch anyway, as a reminder that the number represents a change of length. But the units of length are redundant in such expressions, because they cancel out. When the units of length are left off, strain is seen to be a pure number, which can be expressed as a decimal fraction, a percentage or in parts-per notation. In common solid materials, the change in length is generally a very small fraction of the length, so strain tends to be a very small number. It is very common to express strain in units of micrometre/metre or μm/m. When the units of μm/m are canceled out, strain is expressed as a number followed by μ, the SI prefix all by itself. It is usually clear from the context that μ is used for its SI prefix meaning, which is interchangeable with "× 10−6" or "ppm" (parts per million), and not one of the many other possible meanings for μ. Linear axial strain at single pointIn the case of measuring strain in the selected point of the body, it is expressed as a strain where the distance where
The general case of linear strainFor the body of any shape, subjected to any deformation the values of strain will be different depending on the spatial direction of measurement. Considering the linear deformation in the point A placed at the start of coordinate system and a second point B placed along the x axis, which due to deformation has moved to the point B' the linear strain will be expressed as: Doing similar calculations for axes y and z respective values of εy and εz can be obtained. For any given displacement field
where
Shear strainSimilarly the angular change at any point between two lines crossing this point in a body can be measured as a shear (or shape) strain. Shear strain γ is the limit of ratio of angular difference between any two lines in a body before and after deformation, assuming that the lines lengths are approaching zero. Given a displacement field
Volumetric strainAlthough linear strain ε and shear strain γ completely define the state of deformation of a body, it is also possible to measure other characteristic strain values, like for example volumetric strain, which measures the ratio of change of body's volume. The definition of volumetric strain at selected point is: where
For cartesian coordinate systems, the following expression is a first order approximation: where
The strain tensorUsing above notation for linear and shear strain it is possible to express strain as a strain tensor: using indicial notation or using vector notation: Comparing traditional notation with tensor notation following is obtained for cartesian coordinate system: Then volumetric strain equals: where
gij is a contravariant metric tensor (using tensor notation: Principal strains in two dimensionsBecause the strain tensor is a real symmetric matrix, by singular value decomposition it can be represented as a set of orthogonal eigenvectors, directions along which there is no shear, only stretching or compression. Assuming the two dimensional strain tensor given as: Then principal strains The case of large deformationsAbove reasoning assumes that body is subject to small deformations. It must be rememberred that with increasing deformation the linear strain error increases. For large deformations the strain tensor can be written as: where gij is the metric tensor of body after deformation gij(0) is metric tensor of the undeformed body Engineering strain vs. true strainIn the definition of linear strain (known technically as engineering strain), strains cannot be totaled. Imagine that a body is deformed twice, first by is slightly different from the sum of the strains: and As long as and thus True strain (aka natural strain and logarithmic strain and Hencky's strain), however, can be totaled. This is defined by: and thus where
The engineering strain formula is the series expansion of the true strain formula. See also
Categories: Continuum mechanics | Materials science |
|||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Strain_(materials_science)". A list of authors is available in Wikipedia. |





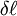 . Then the (relative) strain,
. Then the (relative) strain, 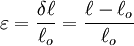
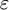 is strain in measured direction
is strain in measured direction
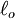 is the original length of the material.
is the original length of the material.
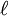 is the current length of the material.
is the current length of the material.
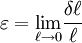
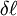 is the length difference for current length
is the length difference for current length 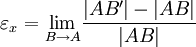
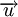 (the values of displacement vectors for all points in the body) the linear strain can be written as:
(the values of displacement vectors for all points in the body) the linear strain can be written as:
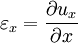 ;
; 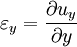 ;
; 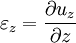
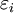 is strain in direction along axis i
is strain in direction along axis i
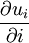 is a differential of
is a differential of 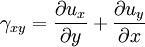 ;
; 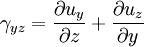 ;
; 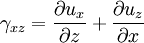
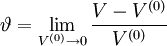
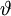 is volumetric strain
is volumetric strain
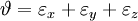
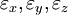 are strains along x, y and z axis
are strains along x, y and z axis
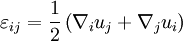
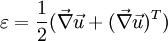
![\varepsilon_{ij}= \left[{\begin{matrix} {\varepsilon _x } & \frac {\gamma _{xy} } {2} & \frac {\gamma _{xz} } {2} \\ \frac {\gamma _{yx} } {2} & {\varepsilon _y } & \frac {\gamma _{yz} } {2} \\ \frac {\gamma _{zx} } {2} & \frac {\gamma _{zy} } {2} & {\varepsilon _z } \end{matrix}}\right]](images/math/f/a/9/fa97350a41b09d97778b2327de78755b.png)
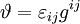
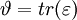 )
)
![\varepsilon_{ij}= \left[{\begin{matrix} {\varepsilon _x } & {\frac {\gamma _{xy}} {2}} \\ {\frac {\gamma _{xy}} {2}} & {\varepsilon _y } \\ \end{matrix}}\right]](images/math/c/c/3/cc31e0372a58e6675ced84d884f33d4a.png)
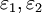 are equal to the eigenvalues of
are equal to the eigenvalues of 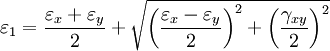
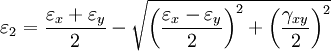
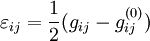
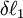 and then by
and then by 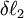 (cumulative deformation). The final strain
(cumulative deformation). The final strain
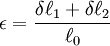
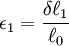
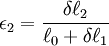
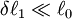 , it is possible to write:
, it is possible to write:
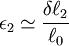
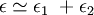
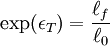
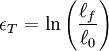
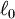 is the original length of the material.
is the original length of the material.
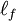 is the final length of the material.
is the final length of the material.


