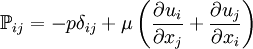To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Newtonian fluid
A Newtonian fluid (named for Isaac Newton) is a fluid that flows like water—its stress versus rate of strain curve is linear and passes through the origin. The constant of proportionality is known as the viscosity. Product highlightA simple equation to describe Newtonian fluid behaviour is where
In common terms, this means the fluid continues to flow, regardless of the forces acting on it. For example, water is Newtonian, because it continues to exemplify fluid properties no matter how fast it is stirred or mixed. Contrast this with a non-Newtonian fluid, in which stirring can leave a "hole" behind (that gradually fills up over time - this behaviour is seen in materials such as pudding, oobleck, or, to a less rigorous extent, sand), or cause the fluid to become thinner, the drop in viscosity causing it to flow more (this is seen in non-drip paints, which brush on easily but become more viscous when on walls). For a Newtonian fluid, the viscosity, by definition, depends only on temperature and pressure (and also the chemical composition of the fluid if the fluid is not a pure substance), not on the forces acting upon it. If the fluid is incompressible and viscosity is constant across the fluid, the equation governing the shear stress, in the Cartesian coordinate system, is with comoving stress tensor where, by the convention of tensor notation,
If a fluid does not obey this relation, it is termed a non-Newtonian fluid, of which there are several types.
Categories: Continuum mechanics | Fluid dynamics |
||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Newtonian_fluid". A list of authors is available in Wikipedia. |





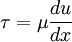
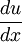 is the velocity gradient perpendicular to the direction of shear [s−1]
is the velocity gradient perpendicular to the direction of shear [s−1]
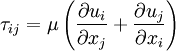
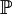 (also written as
(also written as 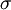 )
)