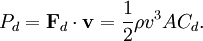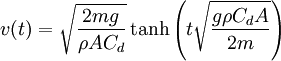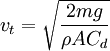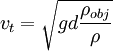To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Drag (physics)
In fluid dynamics, drag (sometimes called resistance) is the force that resists the movement of a solid object through a fluid (a liquid or gas). Drag is made up of friction forces, which act in a direction parallel to the object's surface (primarily along its sides, as friction forces at the front and back cancel themselves out), plus pressure forces, which act in a direction perpendicular to the object's surface. For a solid object moving through a fluid or gas, the drag is the sum of all the aerodynamic or hydrodynamic forces in the direction of the external fluid flow. (Forces perpendicular to this direction are considered lift). It therefore acts to oppose the motion of the object, and in a powered vehicle it is overcome by thrust. In astrodynamics, depending on the situation, atmospheric drag can be regarded as inefficiency requiring expense of additional energy during launch of the space object or as a bonus simplifying return from orbit. Types of drag are generally divided into three categories: parasitic drag, lift-induced drag, and wave drag. Parasitic drag includes form drag, skin friction, and interference drag. Lift-induced drag is only relevant when wings or a lifting body are present, and is therefore usually discussed only in the aviation perspective of drag. Wave drag occurs when a solid object is moving through a fluid at or near the speed of sound in that fluid. The overall drag of an object is characterized by a dimensionless number called the drag coefficient, and is calculated using the drag equation. Assuming a constant drag coefficient, drag will vary as the square of velocity. Thus, the resultant power needed to overcome this drag will vary as the cube of velocity. The standard equation for drag is one half the coefficient of drag multiplied by the fluid density, the cross sectional area of the specified item, and the square of the velocity. Wind resistance or air resistance is a layman's term used to describe drag. Its use is often vague, and is usually used in a relative sense (e.g., A badminton shuttlecock has more wind resistance than a squash ball). Product highlight
Stokes's dragThe equation for viscous resistance or linear drag is appropriate for small objects or particles moving through a fluid at relatively slow speeds. In this case, the force of drag is approximately proportional to velocity, but opposite in direction. [1] The equation for viscous resistance is: where:
When an object falls from rest, its velocity will be which asymptotically approaches the terminal velocity vt = mg / b. For a given b, heavier objects fall faster. For the special case of small spherical objects moving slowly through a viscous fluid (and thus at small Reynolds number), George Gabriel Stokes derived an expression for the drag constant, where:
For example, consider a small sphere with radius r = 0.5 micrometre (diameter = 1.0 µm) moving through water at a velocity v of 10 µm/s. Using 10−3 Pa·s as the dynamic viscosity of water in SI units, we find a drag force of 0.28 pN. This is about the drag force that a bacterium experiences as it swims through water. Drag at high velocityThe Drag equation calculates the force experienced by an object moving through a fluid at relatively large velocity, also called quadratic drag. The equation is attributed to Lord Rayleigh, who originally used where
The reference area A is related to, but not exactly equal to, the area of the projection of the object on a plane perpendicular to the direction of motion (i.e., cross sectional area). Sometimes different reference areas are given for the same object in which case a drag coefficient corresponding to each of these different areas must be given. The reference for a wing would be the plane area rather than the frontal area. PowerThe power required to overcome the aerodynamic drag is given by: Note that the power needed to push an object through a fluid increases as the cube of the velocity. A car cruising on a highway at 50 mph (80 km/h) may require only 10 horsepower (7.5 kW) to overcome air drag, but that same car at 100 mph (160 km/h) requires 80 hp (60 kW). With a doubling of speed the drag (force) quadruples per the formula. Exerting four times the force over a fixed distance produces four times as much work. At twice the speed the work (resulting in displacement over a fixed distance) is done twice as fast. Since power is the rate of doing work, four times the work done in half the time requires eight times the power. It should be emphasized here that the drag equation is an approximation, and does not necessarily give a close approximation in every instance. Thus one should be careful when making assumptions using these equations. Velocity of falling objectThe velocity as a function of time for an object falling through a non-dense medium is roughly given by a function involving a hyperbolic tangent: In other words, velocity asymptotically approaches a maximum value called the Terminal velocity: With all else (gravitational acceleration, density, cross-sectional area, drag constant, etc.) being equal, heavier objects fall faster. For a potato-shaped object of average diameter d and of density ρobj terminal velocity is about For objects of water-like density (raindrops, hail, live objects - animals, birds, insects, etc.) falling in air near the surface of the Earth at sea level, terminal velocity is roughly equal to For example, for human body (d~0.6 m) vt ~70 m/s, for a small animal like a cat (d~0.2 m) vt ~40 m/s, for a small bird (d~0.05 m) vt ~20 m/s, for an insect (d~0.01 m) vt ~9 m/s, for a fog droplet (d~0.0001 m) vt ~0.9 m/s, for a pollen or bacteria (d~0.00001 m) vt ~0.3 m/s and so on. Actual terminal velocity for very small objects (pollen, etc) is even smaller due to the viscosity of air. Terminal velocity is higher for larger creatures, and thus more deadly. A creature such as a mouse falling at its terminal velocity is much more likely to survive impact with the ground than a human falling at its terminal velocity. A small animal such as a cricket impacting at its terminal velocity will probably be unharmed. See also
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Drag_(physics)". A list of authors is available in Wikipedia. |





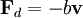
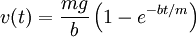
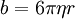
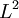 in place of
in place of 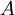 (L being some length). The force on a moving object due to a fluid is:
(L being some length). The force on a moving object due to a fluid is:
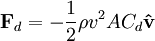
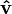 is the unit vector indicating the direction of the velocity (the negative sign indicating the drag is opposite to that of velocity).
is the unit vector indicating the direction of the velocity (the negative sign indicating the drag is opposite to that of velocity).