To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Stokes' law
In 1851, George Gabriel Stokes derived an expression for the frictional force exerted on spherical objects with very small Reynolds numbers (e.g., very small particles) in a continuous viscous fluid by solving the small fluid-mass limit of the generally unsolvable Navier-Stokes equations: Product highlightwhere:
If the particles are falling in the viscous fluid by their own weight, then a terminal velocity, also known as the settling velocity, is reached when this frictional force combined with the buoyant force exactly balance the gravitational force. The resulting settling velocity is given by: where:
See also
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Stokes'_law". A list of authors is available in Wikipedia. |


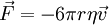



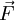 is the frictional force,
is the frictional force,
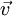 is the particle's velocity.
is the particle's velocity.