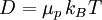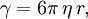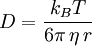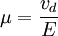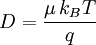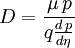Einstein relation (kinetic theory)

In physics (namely, in kinetic theory) the Einstein relation is a previously unexpected connection revealed by Einstein in his 1905 paper on Brownian motion:

Additional recommended knowledge

Guide to balance cleaning: 8 simple steps

Weighing the right way

Essential Laboratory Skills Guide

linking D, the Diffusion constant, and μ_p, the mobility of the particles; where k_B is Boltzmann's constant, and T is the absolute temperature.

The mobility μ_p is the ratio of the particle's terminal drift velocity to an applied force, μ_p = v_d / F.

This equation is an early example of a fluctuation-dissipation relation.

Diffusion of particles

In the limit of low Reynolds number, the mobility μ is the inverse of the drag coefficient γ. For spherical particles of radius r, Stokes' law gives

where η is the viscosity of the medium. Thus the Einstein relation becomes

This equation is also known as the Stokes-Einstein Relation. We can use this to estimate the Diffusion coefficient of a globular protein in aqueous solution: For a 100 kDalton protein, we obtain D ~10^-10 m² s^-1, assuming a "standard" protein density of ~1.2 10³ kg m^-3.

Electrical conduction

When applied to electrical conduction, it is normal to divide through by the charge q of the charge carriers, defining electron mobility (or hole mobility)

where E is the applied electric field; so the Einstein relation becomes

In a semiconductor with an arbitrary density of states the Einstein relation is

where η is the chemical potential and p the particle number