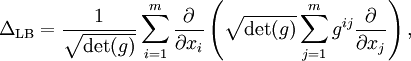To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Brownian motion
Brownian motion (named in honor of the botanist Robert Brown) is the random movement of particles suspended in a fluid or the mathematical model used to describe such random movements, often called a particle theory. The mathematical model of Brownian motion has several real-world applications. An often quoted example is stock market fluctuations. Another example is the evolution of physical characteristics in the fossil record.[citation needed] Brownian motion is among the simplest continuous-time stochastic processes, and it is a limit of both simpler and more complicated stochastic processes (see random walk and Donsker's theorem). This universality is closely related to the universality of the normal distribution. In both cases, it is often mathematical convenience rather than the accuracy of the models that motivates their use. Product highlight
History
The Roman Lucretius's scientific poem On the Nature of Things (c. 60 BC) has a remarkable description of Brownian motion of dust particles (though their movement happens to be mostly due to air currents). He uses this as a proof of the existence of atoms: "Observe what happens when sunbeams are admitted into a building and shed light on its shadowy places. You will see a multitude of tiny particles mingling in a multitude of ways... their dancing is an actual indication of underlying movements of matter that are hidden from our sight... It originates with the atoms which move of themselves [i.e. spontaneously]. Then those small compound bodies that are least removed from the impetus of the atoms are set in motion by the impact of their invisible blows and in turn cannon against slightly larger bodies. So the movement mounts up from the atoms and gradually emerges to the level of our senses, so that those bodies are in motion that we see in sunbeams, moved by blows that remain invisible." Jan Ingenhousz had described the irregular motion of coal dust particles on the surface of alcohol in 1785. Nevertheless Brownian motion is traditionally regarded as discovered by the botanist Robert Brown in 1827. It is believed that Brown was studying pollen particles floating in water under the microscope. He then observed minute particles within the vacuoles of the pollen grains executing a jittery motion. By repeating the experiment with particles of dust, he was able to rule out that the motion was due to pollen particles being 'alive', although the origin of the motion was yet to be explained. The first person to describe the mathematics behind Brownian motion was Thorvald N. Thiele in 1880 in a paper on the method of least squares. This was followed independently by Louis Bachelier in 1900 in his PhD thesis "The theory of speculation", in which he presented a stochastic analysis of the stock and option markets. However, it was Albert Einstein's independent research of the problem in his 1905 paper that brought the solution to the attention of physicists, and presented it as a way to indirectly confirm the existence of atoms and molecules. At that time the atomic nature of matter was still a controversial idea. Einstein and Marian Smoluchowski observed that, if the kinetic theory of fluids was right, then the molecules of water would move at random. Therefore, a small particle would receive a random number of impacts of random strength and from random directions in any short period of time. This random bombardment by the molecules of the fluid would cause a sufficiently small particle to move in exactly the way described by Brown. Theodor Svedberg made important demonstrations of Brownian motion in colloids as Felix Ehrenhaft did for particles of silver in air. Jean Perrin carried out experiments to test the new mathematical models, and his published results finally put an end to the two thousand year-old dispute about the reality of atoms and molecules. Intuitive metaphor for Brownian motionConsider a large balloon of 10 meters in diameter. Imagine this large balloon in a football stadium or any widely crowded area. The balloon is so large that it lies on top of many members of the crowd. Because they are excited, these fans hit the balloon at different times and in different directions with the motions being completely random. In the end, the balloon is pushed in random directions, so it should not move on average. Consider now the force exerted at a certain time. We might have 20 supporters pushing right, and 21 other supporters pushing left, where each supporter is exerting equivalent amounts of force. In this case, the forces exerted from the left side and the right side are imbalanced in favor of the left side; the balloon will move slightly to the left. This imbalance exists at all times, and it causes random motion. If we look at this situation from above, so that we cannot see the supporters, we see the large balloon as a small object animated by erratic movement. Now return to Brown’s pollen particle swimming randomly in water. One molecule of water is about .1 to .2 nm, (a hydrogen-bonded cluster of 300 atoms has a diameter of approximately 3 nm) where the pollen particle is roughly 1 µm in diameter, roughly 10,000 times larger than a water molecule. So, the pollen particle can be considered as a very large balloon constantly being pushed by water molecules. The Brownian motion of particles in a liquid is due to the instantaneous imbalance in the force exerted by the small liquid molecules on the particle. A animation of the Brownian motion concept is available as a Java applet. Modelling the Brownian motion using differential equations
The equations governing Brownian motion relate slightly differently to each of the two definitions of Brownian motion given at the start of this article. Mathematical Brownian motionAn n-dimentional Brownian motion {Xt} is a stochastic process which is characterized by the following 3 properties: 1) The process is continuous 2) The process is nowhere differentiable (a.s.) 3) The increments are Multi-variate Normal where Σ is the covariance matix. One property of a Brownian motion process is that the length of the process is infinite over any length of interval. This means that Brownian motion is purely an abstract concept since no particle can move an infinite distance in a finite length of time. It's important to remember that Brownian motion is used to approximate the movement of particles. The time evolution of the position of the Brownian particle itself can be described approximately by a Langevin equation, an equation which involves a random force field representing the effect of the thermal fluctuations of the solvent on the Brownian particle. On long timescales, the mathematical Brownian motion is well described by a Langevin equation. On small timescales, inertial effects are prevalent in the Langevin equation. However the mathematical brownian motion is exempt of such inertial effects. Note that inertial effects have to be considered in the Langevin equation, otherwise the equation becomes singular, so that simply removing the inertia term from this equation would not yield an exact description, but rather a singular behavior in which the particle doesn't move at all. Physical Brownian motionThe diffusion equation yields an approximation of the time evolution of the probability density function associated to the position of the particle undergoing a Brownian movement under the physical definition. The approximation is valid on short timescales (see Langevin equation for details). The time evolution of the position of the Brownian particle itself is best described using Langevin equation, an equation which involves a random force field representing the effect of the thermal fluctuations of the solvent on the particle. The displacement of a particle undergoing Brownian motion is obtained by solving the diffusion equation under appropriate boundary conditions and finding the rms of the solution. This shows that the displacement varies as the square root of the time, not linearly. Hence why previous experimental results concerning the velocity of Brownian particles gave nonsensical results. A linear time dependence was incorrectly assumed. The Lévy characterization of Brownian motionThe French mathematician Paul Lévy proved the following theorem, which gives a necessary and sufficient condition for a continuous Rn-valued stochastic process X to actually be n-dimensional Brownian motion. Hence, Lévy's condition can actually be used an alternative definition of Brownian motion. Let X = (X1, ..., Xn) be a continuous stochastic process on a probability space (Ω, Σ, P) taking values in Rn. Then the following are equivalent:
Brownian motion on a Riemannian manifold
The infinitesimal generator (and hence characteristic operator) of a Brownian motion on Rn is easily calculated to be ½Δ, where Δ denotes the Laplace operator. This observation is useful in defining Brownian motion on an m-dimensional Riemannian manifold (M, g): a Brownian motion on M is defined to be a diffusion on M whose characteristic operator where [gij] = [gij]−1 in the sense of the inverse of a square matrix. Cultural usesThe awareness of Brownian motion as a stochastic process is referred to in science fiction. In Douglas Adams's The Hitchhiker's Guide to the Galaxy, Brownian motion is used to create (or rather calculate) the Infinite Improbability Drive that powers the spaceship Heart of Gold. The Brownian motion generator is a really hot cup of tea. In Murray Leinster's short story, A Logic Named Joe, the logic (computer) suggests building a perpetual motion machine using Brownian motion. It also appears in other novels. In Julio Cortazar's novel Rayuela, Brownian motion is used to describe travelers in Paris at night. It also appears in a famous/notorious essay by Constance Penley, "Brownian Motion: Women, Tactics, and Technology". See also
References
Categories: Statistical mechanics | Colloidal chemistry |
|||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Brownian_motion". A list of authors is available in Wikipedia. |





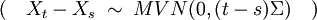
 in local coordinates xi, 1 ≤ i ≤ m, is given by ½ΔLB, where ΔLB is the Laplace-Beltrami operator given in local coordinates by
in local coordinates xi, 1 ≤ i ≤ m, is given by ½ΔLB, where ΔLB is the Laplace-Beltrami operator given in local coordinates by