To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Local time (mathematics)In the mathematical theory of stochastic processes, local time is a property of diffusion processes like Brownian motion that characterizes the time a particle has spent at a given level. Local time is very useful and often appears in various stochastic integration formulas if the integrand is not sufficiently smooth, for example in Tanaka's formula. Product highlightStrict definitionFormally, the definition of the local time is where b(s) is the diffusion process and δ is the Dirac delta function. It is a notion invented by P. Lévy. The basic idea is that which explains why it is called the local time of b at x. See also
References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Local_time_(mathematics)". A list of authors is available in Wikipedia. |





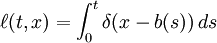
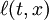 is a (rescaled) measure of how much time
is a (rescaled) measure of how much time