To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Diffusion equationThe diffusion equation is a partial differential equation which describes density fluctuations in a material undergoing diffusion. It is also used to describe processes exhibiting diffusive-like behaviour, for instance the 'diffusion' of alleles in a population in population genetics. Product highlightThe equation is usually written as: where also called the heat equation. More generally, when D is a symmetric positive definite matrix, the equation describes anisotropic diffusion. DerivationThe diffusion equation can be derived in a straightforward way from the continuity equation, which states that a change in density in any part of the system is due to inflow and outflow of material into and out of that part of the system. Effectively, no material is created or destroyed:
where
See also |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Diffusion_equation". A list of authors is available in Wikipedia. |





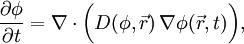
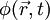 is the
is the 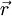 and time
and time 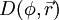 is the collective diffusion coefficient for density
is the collective diffusion coefficient for density  represents the vector differential operator del acting on the space coordinates. If the diffusion coefficient depends on the density then the equation is nonlinear, otherwise it is linear. If
represents the vector differential operator del acting on the space coordinates. If the diffusion coefficient depends on the density then the equation is nonlinear, otherwise it is linear. If 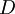 is constant, then the equation reduces to the following linear equation:
is constant, then the equation reduces to the following linear equation:
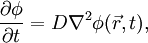
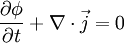 ,
,
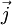 is the flux of the diffusing material. The diffusion equation can be obtained easily from this when combined with the phenomenological Fick's first law, which assumes that the flux of the diffusing material in any part of the system is proportional to the local density gradient:
is the flux of the diffusing material. The diffusion equation can be obtained easily from this when combined with the phenomenological Fick's first law, which assumes that the flux of the diffusing material in any part of the system is proportional to the local density gradient:
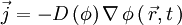 .
.


