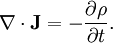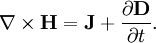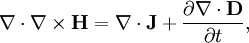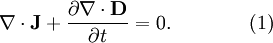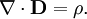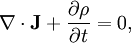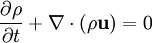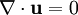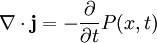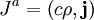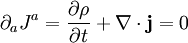To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Continuity equationA continuity equation is a differential equation that describes the conservative transport of some kind of quantity. Since mass, energy, momentum, and other natural quantities are conserved, a vast variety of physics may be described with continuity equations. All the examples of continuity equations below express the same idea. Continuity equations are the (stronger) local form of conservation laws. Product highlight
GeneralThe general form for a continuity equation is where Electromagnetic theoryIn electromagnetic theory, the continuity equation is derived from two of Maxwell's equations. It states that the divergence of the current density is equal to the negative rate of change of the charge density, DerivationOne of Maxwell's equations, Ampère's law, states that Taking the divergence of both sides results in but the divergence of a curl is zero, so that Another one of Maxwell's equations, Gauss's law, states that Substitute this into equation (1) to obtain which is the continuity equation. InterpretationCurrent density is the movement of charge density. The continuity equation says that if charge is moving out of a differential volume (i.e. divergence of current density is positive) then the amount of charge within that volume is going to decrease, so the rate of change of charge density is negative. Therefore the continuity equation amounts to a conservation of charge. Fluid dynamicsIn fluid dynamics, a continuity equation is a mathematical statement for conservation of mass. Its differential form is where ρ is fluid density, t is time, and u is fluid velocity. If ρ is a constant, as in the case of incompressible flow, the mass continuity equation simplifies to a volume continuity equation: which means that the divergence of velocity field is zero everywhere. Physically, it is equivalent to saying that the local volume dilation rate is zero. Further, the Navier-Stokes equations form a vector continuity equation describing the conservation of linear momentum. Quantum mechanicsIn quantum mechanics, the conservation of probability also yields a continuity equation. Let P(x, t) be a probability density function and write where J is probability flux. Four-currentsConservation of a current is expressed compactly as the Lorentz invariant divergence of a four-current: where
See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Continuity_equation". A list of authors is available in Wikipedia. |





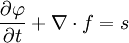
 is some quantity, ƒ is a function describing the flux of
is some quantity, ƒ is a function describing the flux of