To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Incompressible flowIn fluid mechanics or more generally continuum mechanics, an incompressible flow is solid or fluid flow in which the divergence of velocity is zero. This is more precisely termed isochoric flow. It is an idealization used to simplify analysis. In reality, all materials are compressible to some extent. Note that isochoric refers to flow, not the material property. This means that under certain circumstances, a compressible material can undergo (nearly) incompressible flow. However, by making the 'incompressible' assumption, the governing equations of material flow can be simplified significantly. The equation describing an incompressible (isochoric) flow,
where The continuity equation states that, This can be expressed via the material derivative as Since ρ > 0, we see that a flow is incompressible if and only if, that is, the mass density is constant following the material element. Product highlight
Relation to compressibility factorIn some fields, a measure of the incompressibility of a flow is the change in density as a result of the pressure variations. This is best expressed in terms of the compressibility factor If the compressibility factor is acceptably small, the flow is considered to be incompressible. Relation to solenoidal fieldAn incompressible flow is described by a velocity field which is solenoidal. But a solenoidal field, besides having a zero divergence, also has the additional connotation of having non-zero curl (i.e., rotational component). Otherwise, if an incompressible flow also has a curl of zero, so that it is also irrotational, then the velocity field is actually Laplacian. Difference between incompressible flow and materialAs defined earlier, an incompressible (isochoric) flow is the one in which
This is equivalent to saying that i.e. the material derivative of the density is zero. Thus if we follow a material element, it's mass density will remain constant. Note that the material derivative consists of two terms. The first term On the other hand, a homogeneous, incompressible material is defined as one which has constant density throughout. For such a material, ρ = constant. This implies that,
From the continuity equation it follows that Thus homogeneous materials always undergo flow that is incompressible, but the converse is not true. It is common to find references where the author mentions incompressible flow and assumes that density is constant. Even though this is technically incorrect, it is an accepted practice. One of the advantages of using the incompressible material assumption over the incompressible flow assumption is in the momentum equation where the kinematic viscosity (
See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Incompressible_flow". A list of authors is available in Wikipedia. |


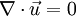 ,
,
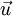 is the velocity of the material.
is the velocity of the material.
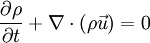
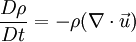
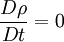



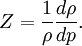
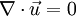 .
.
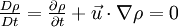
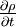 is the unsteady term and describes how the density of the material element changes with time. This term is also know as the unsteady term. The second term,
is the unsteady term and describes how the density of the material element changes with time. This term is also know as the unsteady term. The second term, 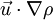 describes the changes in the density as the material element moves from one point to another. This is the convection or the advection term. For a flow to be incompressible the sum of these terms should be zero.
describes the changes in the density as the material element moves from one point to another. This is the convection or the advection term. For a flow to be incompressible the sum of these terms should be zero.
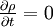 and
and
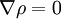 independently.
independently.
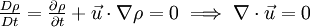
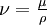 ) can be assumed to be constant. The subtlety above is frequently a source of confusion. Therefore many people prefer to refer explicitly to incompressible materials or isochoric flow when being descriptive about the mechanics.
) can be assumed to be constant. The subtlety above is frequently a source of confusion. Therefore many people prefer to refer explicitly to incompressible materials or isochoric flow when being descriptive about the mechanics.


