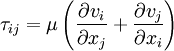To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Fluid mechanics
Fluid mechanics is the study of how fluids move and the forces on them. (Fluids include liquids and gases.) Fluid mechanics can be divided into fluid statics, the study of fluids at rest, and fluid dynamics, the study of fluids in motion. It is a branch of continuum mechanics, a subject which models matter without using the information that it is made out of atoms. The study of fluid mechanics goes back at least to the days of ancient Greece, when Archimedes made a beginning on fluid statics. However, fluid mechanics, especially fluid dynamics, is an active field of research with many unsolved or partly solved problems. Fluid mechanics can be mathematically complex. Sometimes it can best be solved by numerical methods, typically using computers. A modern discipline, called Computational Fluid Dynamics (CFD), is devoted to this approach to solving fluid mechanics problems. Product highlight
Relationship to continuum mechanicsFluid mechanics is a subdiscipline of continuum mechanics, as illustrated in the following table.
In a mechanical view, a fluid is a substance that does not support tangential stress; that is why a fluid in rest has the shape of their containing vessel.And fluid in rest have zero shear stress AssumptionsLike any mathematical model of the real world, fluid mechanics makes some basic assumptions about the materials being studied. These assumptions are turned into equations that must be satisfied if the assumptions are to hold true. For example, consider an incompressible fluid in three dimensions. The assumption that mass is conserved means that for any fixed closed surface (such as a sphere) the rate of mass passing from outside to inside the surface must be the same as rate of mass passing the other way. (Alternatively, the mass inside remains constant, as does the mass outside). This can be turned into an integral equation over the surface. Fluid mechanics assumes that every fluid obeys the following:
Further, it is often useful (and realistic) to assume a fluid is incompressible - that is, the density of the fluid does not change. Liquids can often be modelled as incompressible fluids, whereas gases cannot. Similarly, it can sometimes be assumed that the viscosity of the fluid is zero (the fluid is inviscid). Gases can often be assumed to be inviscid. If a fluid is viscous, and its flow contained in some way (e.g. in a pipe), then the flow at the boundary must have zero velocity. For a viscous fluid, if the boundary is not porous, the shear forces between the fluid and the boundary results also in a zero velocity for the fluid at the boundary. This is called the no-slip condition. For a porous media otherwise, in the frontier of the containing vessel, the slip condition is not zero velocity, and the fluid has a discontinuous velocity field between the free fluid and the fluid in the porous media (this is related to the Beavers and Joseph condition). The continuum hypothesisFluids are composed of molecules that collide with one another and solid objects. The continuum assumption, however, considers fluids to be continuous. That is, properties such as density, pressure, temperature, and velocity are taken to be well-defined at "infinitely" small points, defining a REV (Reference Element of Volume), at the geometric order of the distance between two adjacent molecules of fluid. Properties are assumed to vary continuously from one point to another, and are averaged values in the REV. The fact that the fluid is made up of discrete molecules is ignored. The continuum hypothesis is basically an approximation, in the same way planets are approximated by point particles when dealing with celestial mechanics, and therefore results in approximate solutions. Consequently, assumption of the continuum hypothesis can lead to results which are not of desired accuracy. That said, under the right circumstances, the continuum hypothesis produces extremely accurate results. Those problems for which the continuum hypothesis does not allow solutions of desired accuracy are solved using statistical mechanics. To determine whether or not to use conventional fluid dynamics or statistical mechanics, the Knudsen number is evaluated for the problem. The Knudsen number is defined as the ratio of the molecular mean free path length to a certain representative physical length scale. This length scale could be, for example, the radius of a body in a fluid. (More simply, the Knudsen number is how many times its own diameter a particle will travel on average before hitting another particle). Problems with Knudsen numbers at or above unity are best evaluated using statistical mechanics for reliable solutions. Navier-Stokes equationsMain article: Navier-Stokes equations The Navier-Stokes equations (named after Claude-Louis Navier and George Gabriel Stokes) are the set of equations that describe the motion of fluid substances such as liquids and gases. These equations state that changes in momentum (acceleration) of fluid particles depend only on the external pressure and internal viscous forces (similar to friction) acting on the fluid. Thus, the Navier-Stokes equations describe the balance of forces acting at any given region of the fluid. The Navier-Stokes equations are differential equations which describe the motion of a fluid. Such equations establish relations among the rates of change the variables of interest. For example, the Navier-Stokes equations for an ideal fluid with zero viscosity states that acceleration (the rate of change of velocity) is proportional to the derivative of internal pressure. This means that solutions of the Navier-Stokes equations for a given physical problem must be sought with the help of calculus. In practical terms only the simplest cases can be solved exactly in this way. These cases generally involve non-turbulent, steady flow (flow does not change with time) in which the Reynolds number is less. For more complex situations, such as global weather systems like El Niño or lift in a wing, solutions of the Navier-Stokes equations can currently only be found with the help of computers. This is a field of sciences by its own called computational fluid dynamics. General form of the equationThe general form of the Navier-Stokes equations for the conservation of momentum is: where
Unless the fluid is made up of spinning degrees of freedom like vortices, where
The above is actually a set of three equations, one per dimension. By themselves, these aren't sufficient to produce a solution. However, adding conservation of mass and appropriate boundary conditions to the system of equations produces a solvable set of equations. Newtonian vs. non-Newtonian fluidsA Newtonian fluid (named after Isaac Newton) is defined to be a fluid whose shear stress is linearly proportional to the velocity gradient in the direction perpendicular to the plane of shear. This definition means regardless of the forces acting on a fluid, it continues to flow. For example, water is a Newtonian fluid, because it continues to display fluid properties no matter how much it is stirred or mixed. A slightly less rigorous definition is that the drag of a small object being moved through the fluid is proportional to the force applied to the object. (Compare friction). By contrast, stirring a non-Newtonian fluid can leave a "hole" behind. This will gradually fill up over time - this behaviour is seen in materials such as pudding, oobleck, or sand (although sand isn't strictly a fluid). Alternativley, stirring a non-Newtonian fluid can cause the viscosity to decrease, so the fluid appears "thinner" (this is seen in non-drip paints). There are many types of non-Newtonian fluids, as they are defined to be something that fails to obey a particular property. Equations for a Newtonian fluidMain article: Newtonian fluid The constant of proportionality between the shear stress and the velocity gradient is known as the viscosity. A simple equation to describe Newtonian fluid behaviour is where
For a Newtonian fluid, the viscosity, by definition, depends only on temperature and pressure, not on the forces acting upon it. If the fluid is incompressible and viscosity is constant across the fluid, the equation governing the shear stress (in Cartesian coordinates) is where
If a fluid does not obey this relation, it is termed a non-Newtonian fluid, of which there are several types. See also
References
Categories: Continuum mechanics | Fluid mechanics |
|||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Fluid_mechanics". A list of authors is available in Wikipedia. | |||||||||||||||||||||||||||





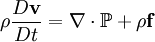
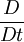 is the
is the 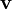 is the velocity vector,
is the velocity vector,
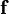 is the body force vector, and
is the body force vector, and
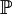 is a tensor that represents the surface forces applied on a fluid particle (the comoving stress tensor).
is a tensor that represents the surface forces applied on a fluid particle (the comoving stress tensor).
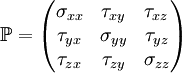
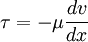
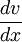 is the velocity gradient perpendicular to the direction of shear
is the velocity gradient perpendicular to the direction of shear