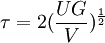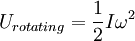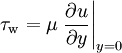To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Shear stressShear stress is a stress state where the stress is parallel or tangential to a face of the material, as opposed to normal stress when the stress is perpendicular to the face. The variable used to denote shear stress is τ (tau). There are two forms of shear stress: direct shear and beam shear. Physical quantities of shear stress are measured in force divided by area (newtons per square meter in SI units). This unit is called the pascal (Pa). Shear stress is also commonly measured in pounds-force per square inch or kilopounds-force per square inch. The area is always the area resisting the shear, and not the area that the force is acting upon. These two areas are always at right angles. Product highlight
Direct ShearThe formula for direct shear is:
Structural members that are often considered to be in pure shear stress are riveted and bolted joints. For bolts and rivets the two plates must be touching, and locked together for the pure shear case to apply. Welds may also be subjected to pure shear stress depending on the location and loading. Cantilever beams, consoles and column heads are subject to composite loading, consisting of shear, tensile and compressive stress. Beam ShearThe formula for shear stress in a beam is:
Semi-monocoque shearShear stresses within a semi-monocoque structure may be calculated by idealizing the cross-section of the structure into a set of stringers (carrying only axial loads) and webs (carrying only shear flows). Dividing the shear flow by the thickness of a given portion of the semi-monocoque structure yields the shear stress. Thus, the maximum shear stress will occur either in the web of maximum shear flow or minimum thickness. Also constructions in soil can fail due to shear; e.g., the weight of an earth-filled dam or dike may cause the subsoil to collapse, like a small landslide. Shear stress is relevant to the motion of fluids upon surfaces, which result in the generation of shear stress. Particularly, the laminar fluid flow over the surface has a zero velocity and shear stress occurs between the zero-velocity surface and the higher-velocity flow away from the surface. Impact ShearThe maximum shear stress created in a solid round bar subject to impact is given. The equation is:
Where:
And:
Uapplied = Tθdisplaced U = Urotating + Uapplied
Shear Stress in FluidsA viscous fluid (including air and water) moving along a solid boundary will incur a shear stress on that boundary. The no-slip condition dictates that the speed of the fluid at the boundary (relative to the boundary) is 0, but at some height from the boundary the flow speed must equal that of the fluid. The region between these two points is aptly named the boundary layer. The shear stress is imparted onto the boundary as a result of this loss of velocity and can be expressed as where μ is the dynamic viscosity of the fluid, u is the velocity of the fluid along the boundary, and y is the height off the boundary. Diverging Fringe Shear Stress SensorThis relationship can be exploited to measure the wall shear stress. If a sensor could directly measure the gradient of the velocity profile at the wall, then multiplying by the dynamic viscosity would yield the shear stress. Such a sensor was demonstrated by A. A. Naqwi and W. C. Reynolds[1]. The interference pattern generated by sending a beam of light through two parallel slits forms a network of linearly diverging fringes that seem to originate from the plane of the two slits (see double-slit experiment). As a particle in a fluid passes through the fringes, a receiver detects the reflection of the fringe pattern. The signal can be processed, and knowing the fringe angle, the height and velocity of the particle can be extrapolated. References
See also
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Shear_stress". A list of authors is available in Wikipedia. |





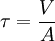 , where
, where
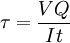 , where
, where