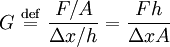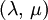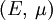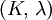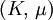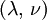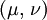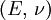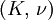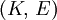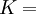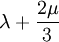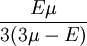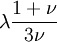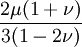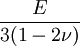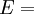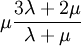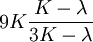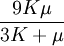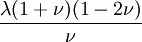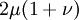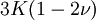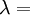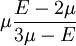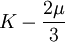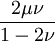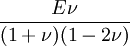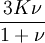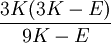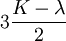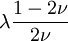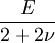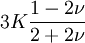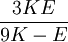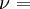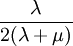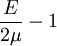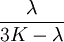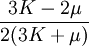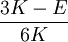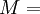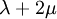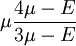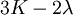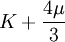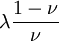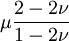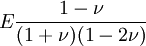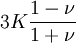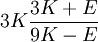To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Shear modulusIn materials science, shear modulus, G, or sometimes S or μ, sometimes referred to as the modulus of rigidity, is defined as the ratio of shear stress to the shear strain:[1]
Product highlightwhere
Shear modulus is usually measured in GPa (gigapascals) or ksi (thousands of pounds per square inch).
ExplanationThe shear modulus is one of several quantities for measuring the strength of materials. All of them arise in the generalized Hooke's law. Young's modulus describes the material's response to linear strain (like pulling on the ends of a wire), the bulk modulus describes the material's response to uniform pressure, and the shear modulus describes the material's response to shearing strains. Anisotropic materials such as wood and paper exhibit differing material response to stress or strain when tested in different directions. The shear modulus is concerned with the deformation of a solid when it experiences a force parallel to one of its surfaces while its opposite face experiences an opposing force (such as friction). In the case of an object that's shaped like a rectangular prism, it will deform into a parallelepiped. In solids, there are two kinds of sound waves, pressure waves and shear waves. The speed of sound for shear waves is controlled by the shear modulus. See alsoReferences
Categories: Materials science | Continuum mechanics |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Shear_modulus". A list of authors is available in Wikipedia. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||