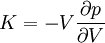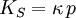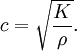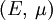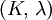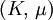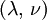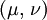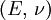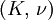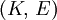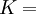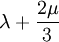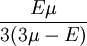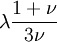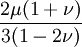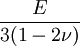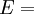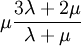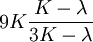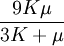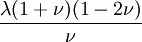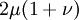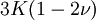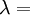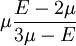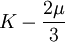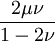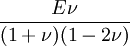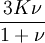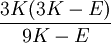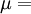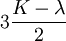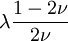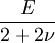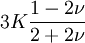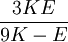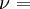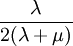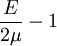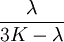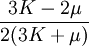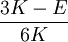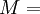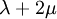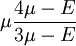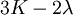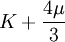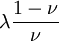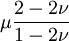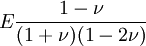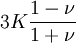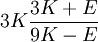My watch list

Bulk modulus

Bulk modulus values for some example substances
Water	2.2×10⁹ Pa (value increases at higher pressures)
Air	1.42×10⁵ Pa (adiabatic bulk modulus)
Air	1.01×10⁵ Pa (constant temperature bulk modulus)
Steel	1.6×10¹¹ Pa
Glass	3.5×10¹⁰ to 5.5×10¹⁰ Pa
Solid helium	5×10⁷ Pa (approximate)

Additional recommended knowledge

How to ensure accurate weighing results every day?

Daily Sensitivity Test

What is the Correct Way to Check Repeatability in Balances?

The bulk modulus (K) of a substance essentially measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to effect a given relative decrease in volume.

As an example, suppose an iron cannon ball with bulk modulus 160 GPa (gigapascal) is to be reduced in volume by 0.5%. This requires a pressure increase of 0.005×160 GPa = 0.8 GPa. If the cannon ball is subjected to a pressure increase of only 100 MPa, it will decrease in volume by a factor of 100 MPa/160 GPa = 0.000625, or 0.0625%.

The bulk modulus K can be formally defined by the equation:

$K=-V\frac{\partial p}{\partial V}$

where p is pressure, V is volume, and ∂p/∂V denotes the partial derivative of pressure with respect to volume. The inverse of the bulk modulus gives a substance's compressibility.

Other moduli describe the material's response (strain) to other kinds of stress: the shear modulus describes the response to shear, and Young's modulus describes the response to linear strain. For a fluid, only the bulk modulus is meaningful. For an anisotropic solid such as wood or paper, these three moduli do not contain enough information to describe its behaviour, and one must use the full generalized Hooke's law.

Strictly speaking, the bulk modulus is a thermodynamic quantity, and it is necessary to specify how the temperature varies in order to specify a bulk modulus: constant-temperature ( $K T$ ), constant-enthalpy (adiabatic $K S$ ), and other variations are possible. In practice, such distinctions are usually only relevant for gases.

For a gas, the adiabatic bulk modulus $K S$ is approximately given by

$K_S=\kappa\, p$

where

κ is the adiabatic index, sometimes called γ.

p is the pressure.

In a fluid, the bulk modulus K and the density ρ determine the speed of sound c (pressure waves), according to the formula

$c=\sqrt{\frac{K}{\rho}}.$

Solids can also sustain transverse waves, for these one additional elastic modulus, for example the shear modulus, is needed to determine wave speeds.

References

Bulk Elastic Properties on hyperphysics at Georgia State University

^ Bulk modulus calculation of glasses

v • d • e Elastic moduli for homogeneous isotropic materials

Conversion formulas
Homogeneous isotropic linear elastic materials have their elastic properties uniquely determined by any two moduli among these, thus given any two, any other of the elastic moduli can be calculated according to these formulas.
	$(\lambda,\,\mu)$	$(E,\,\mu)$	$(K,\,\lambda)$	$(K,\,\mu)$	$(\lambda,\,\nu)$	$(\mu,\,\nu)$	$(E,\,\nu)$	$(K,\, \nu)$	$(K,\,E)$
$K=\,$	$\lambda+ \frac{2\mu}{3}$	$\frac{E\mu}{3(3\mu-E)}$			$\lambda\frac{1+\nu}{3\nu}$	$\frac{2\mu(1+\nu)}{3(1-2\nu)}$	$\frac{E}{3(1-2\nu)}$
$E=\,$	$\mu\frac{3\lambda + 2\mu}{\lambda + \mu}$		$9K\frac{K-\lambda}{3K-\lambda}$	$\frac{9K\mu}{3K+\mu}$	$\frac{\lambda(1+\nu)(1-2\nu)}{\nu}$	$2\mu(1+\nu)\,$		$3K(1-2\nu)\,$
$\lambda=\,$		$\mu\frac{E-2\mu}{3\mu-E}$		$K-\frac{2\mu}{3}$		$\frac{2 \mu \nu}{1-2\nu}$	$\frac{E\nu}{(1+\nu)(1-2\nu)}$	$\frac{3K\nu}{1+\nu}$	$\frac{3K(3K-E)}{9K-E}$
$\mu=\,$			$3\frac{K-\lambda}{2}$		$\lambda\frac{1-2\nu}{2\nu}$		$\frac{E}{2+2\nu}$	$3K\frac{1-2\nu}{2+2\nu}$	$\frac{3KE}{9K-E}$
$\nu=\,$	$\frac{\lambda}{2(\lambda + \mu)}$	$\frac{E}{2\mu}-1$	$\frac{\lambda}{3K-\lambda}$	$\frac{3K-2\mu}{2(3K+\mu)}$					$\frac{3K-E}{6K}$
$M=\,$	$\lambda+2\mu\,$	$\mu\frac{4\mu-E}{3\mu-E}$	$3K-2\lambda\,$	$K+\frac{4\mu}{3}$	$\lambda \frac{1-\nu}{\nu}$	$\mu\frac{2-2\nu}{1-2\nu}$	$E\frac{1-\nu}{(1+\nu)(1-2\nu)}$	$3K\frac{1-\nu}{1+\nu}$	$3K\frac{3K+E}{9K-E}$