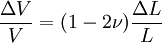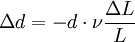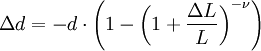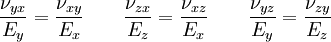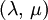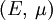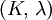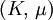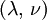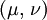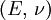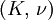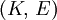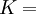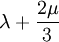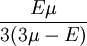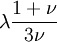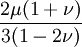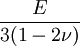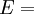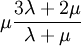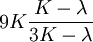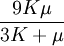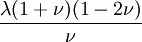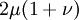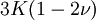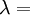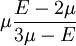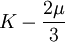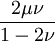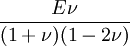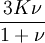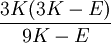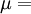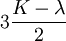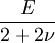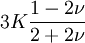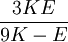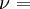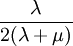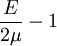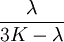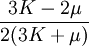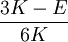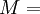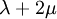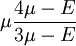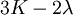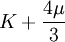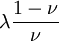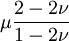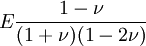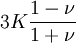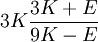To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Poisson's ratio
When a sample of material is stretched in one direction, it tends to get thinner in the other two directions. Poisson's ratio (ν), named after Simeon Poisson, is a measure of this tendency. Poisson's ratio is the ratio of the relative contraction strain, or transverse strain (normal to the applied load), divided by the relative extension strain, or axial strain (in the direction of the applied load). For a perfectly incompressible material deformed elastically at small strains, the Poisson's ratio would be exactly 0.5. Most materials have ν between 0.0 and 0.5. Cork is close to 0.0, most steels are around 0.3, and rubber is almost 0.5. Some materials, mostly polymer foams, have a negative Poisson's ratio; if these auxetic materials are stretched in one direction, they become thicker in perpendicular directions. There are also materials with unusually high (above 0.5) Poisson ratios; when stretched, their volume decreases. Assuming that the material is compressed along the axial direction: where
Product highlight
Generalized Hooke's lawFor an isotropic material, the deformation of a material in the direction of one axis will produce a deformation of the material along the other axes in three dimensions. Thus it is possible to generalize Hooke's Law into three dimensions: where
Volumetric changeThe relative change of volume ΔV/V due to the stretch of the material can be calculated using a simplified formula (only for small deformations): where
Width changeIf a rod with diameter (or width, or thickness) d and length L is subject to tension so that its length will change by ΔL then its diameter d will change by (the value is negative, because the diameter will decrease with increasing length): The above formula is true only in the case of small deformations; if deformations are large then the following (more precise) formula can be used: where
Orthotropic materialsFor Orthotropic material, such as wood in which Poisson's ratio is different in each direction (x, y and z axis) the relation between Young's modulus and Poisson's ratio is described as follows: where
Poisson's ratio values for different materials
See also
References
Categories: Solid mechanics | Materials science |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Poisson's_ratio". A list of authors is available in Wikipedia. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


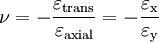
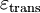 is transverse strain (negative for axial tension, positive for axial compression)
is transverse strain (negative for axial tension, positive for axial compression)
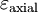 is axial strain (positive for axial tension, negative for axial compression).
is axial strain (positive for axial tension, negative for axial compression).



![\varepsilon_x = \frac {1}{E} \left [ \sigma_x - \nu \left ( \sigma_y + \sigma_z \right ) \right ]](images/math/f/9/6/f96cf49b267ede9e47bbfb3b7249873f.png)
![\varepsilon_y = \frac {1}{E} \left [ \sigma_y - \nu \left ( \sigma_x + \sigma_z \right ) \right ]](images/math/1/6/7/1677af686fe5f6b3ee69c910b84445ee.png)
![\varepsilon_z = \frac {1}{E} \left [ \sigma_z - \nu \left ( \sigma_x + \sigma_y \right ) \right ]](images/math/2/f/c/2fc0dc49396a59c7df5f108a78d82d96.png)
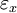 ,
, 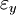 and
and 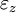 are
are