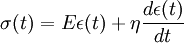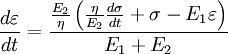To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Viscoelasticity
Viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. Viscous materials, like honey, resist shear flow and strain linearly with time when a stress is applied. Elastic materials strain instantaneously when stretched and just as quickly return to their original state once the stress is removed. Viscoelastic materials have elements of both of these properties and, as such, exhibit time dependent strain. Whereas elasticity is usually the result of bond stretching along crystallographic planes in an ordered solid, viscoelasticity is the result of the diffusion of atoms or molecules inside of an amorphous material [1]. Product highlight
BackgroundIn the nineteenth century, physicists such as Maxwell, Boltzmann, and Kelvin researched and experimented with creep and recovery of glasses, metals, and rubbers [2]. Viscoelasticity was further examined in the late twentieth century when synthetic polymers were engineered and used in a variety of applications [2]. Viscoelasticty calculations depend heavily on the viscosity variable, η. The inverse of η is also known as fluidity, φ. The value of either can be derived as a function of temperature or as a given value (ie for a dashpot) [1]. Depending on the change of strain rate versus stress inside a material the viscosity can be categorized as having a linear, non-linear, or plastic response. When a material exhibits a linear response it is categorized as a Newtonian material [1]. In this case the stress is linearly proportional to the strain rate. If the material exhibits a non-linear response to the strain rate, it is categorized as Non-Newtonian fluid. There is also an interesting case where the viscosity decreases as the shear/strain rate remains constant. A material which exhibits this type of behavior is known as thixotropic [1]. In addition, when the stress is independent of this strain rate, the material exhibits plastic deformation [1]. Many viscoelastic materials exhibit rubber like behavior explained by the thermodynamic theory of polymer elasticity. Some examples of viscoelastic materials include amorphous polymers, semicrystalline polymers, biopolymers, and metals at very high temperatures. Cracking occurs when the strain is applied quickly and outside of the elastic limit. A viscoelastic material has the following properties:
Elastic behavior versus viscoelastic behavior
Unlike purely elastic substances, a viscoelastic substance has an elastic component and a viscous component. The viscosity of a viscoelastic substance gives the substance a strain rate dependent on time[1]. Purely elastic materials do not dissipate energy (heat) when a load is applied, then removed[1]. However, a viscoelastic substance loses energy when a load is applied, then removed. Hysteresis is observed in the stress-strain curve, with the area of the loop being equal to the energy lost during the loading cycle[1]. Since viscosity is the resistance to thermally activated plastic deformation, a viscous material will lose energy through a loading cycle. Plastic deformation results in lost energy, which is uncharacteristic of a purely elastic material's reaction to a loading cycle[1]. Specifically, viscoelasticity is a molecular rearrangement. When a stress is applied to a viscoelastic material such as a polymer, parts of the long polymer chain change position. This movement or rearrangement is called Creep. Polymers remain a solid material even when these parts of their chains are rearranging in order to accompany the stress, and as this occurs, it creates a back stress in the material. When the back stress is the same magnitude as the applied stress, the material no longer creeps. When the original stress is taken away, the accumulated back stresses will cause the polymer to return to its original form. The material creeps, which gives the prefix visco-, and the material fully recovers, which gives the suffix -elasticity[2]. Types of viscoelasticityLinear viscoelasticity is when the function is separable in both creep response and load. All linear viscoelastic models can be represented by a Volterra equation connecting stress and strain: or where
Linear viscoelasticity is usually applicable only for small deformations. Nonlinear viscoelasticity is when the function is not separable. It is usually happens when the deformations are large or if the material changes its properties under deformations. An anelastic material is a special case of a viscoelastic material: an anelastic material will NOT fully recover to its original state on the removal of load. Dynamic modulusViscoelasticity is studied using dynamic mechanical analysis. When we apply a small oscillatory strain and measure the resulting stress.
Complex Dynamic modulus G can be used to represent the relations between the oscillating stress and strain:
where i = sqrt( − 1); G' is the storage modulus and G'' is the loss modulus: where σ0 and Constitutive models of linear viscoelasticityViscoelastic materials, such as amorphous polymers, semicrystalline polymers, and biopolymers, can be modeled in order to determine their stress or strain interactions as well as their temporal dependencies. These models, which include the Maxwell model, the Kelvin-Voigt model, and the Standard Linear Solid Model, are used to predict a material's response under different loading conditions. Viscoelastic behavior is comprised of elastic and viscous components modeled as linear combinations of springs and dashpots, respectively. Each model differs in the arrangement of these elements, and all of these viscoelastic models can be equivalently modeled as electrical circuits. The elastic modulus of a spring is analogous to a circuit's resistance and the viscosity of a dashpot to a capacitor. The elastic components, as previously mentioned, can be modeled as springs of elastic constant E, given the formula: where σ is the stress, E is the elastic modulus of the material, and ε is the strain that occurs under the given stress, similar to Hooke's Law. The viscous components can be modeled as dashpots such that the stress-strain rate relationship can be given as, where σ is the stress, η is the viscosity of the material, and dε/dt is the time derivative of strain. The relationship between stress and strain can be simplified for specific stress rates. For high stress states/short time periods, the time derivative components of the stress-strain relationship dominate. A dashpots resists changes in length, and in a high stress state it can be approximated as a rigid rod. Since a rigid rod cannot be stretched past its original length, no strain is added to the system[3] Conversely, for low stress states/longer time periods, the time derivative components are negligible and the dashpot can be effectively removed from the system - an "open" circuit. As a result, only the spring connected in parallel to the dashpot will contribute to the total strain in the system[3] Maxwell modelThe Maxwell model can be represented by a purely viscous damper and a purely elastic spring connected in series, as shown in the diagram. The model can be represented by the following equation:
The model represents a liquid (able to have irreversible deformations) with some additional reversible (elastic) deformations. If put under a constant strain, the stresses gradually relax. When a material is put under a constant stress, the strain has two components as per the Maxwell Model. First, an elastic component occurs instantaneously, corresponding to the spring, and relaxes immediately upon release of the stress. The second is a viscous component that grows with time as long as the stress is applied. The Maxwell model predicts that stress decays exponentially with time, which is accurate for most polymers. It is important to note limitations of such a model, as it is unable to predict creep in materials based on a simple dashpot and spring connected in series. The Maxwell model for creep or constant-stress conditions postulates that strain will increase linearly with time. However, polymers for the most part show the strain rate to be decreasing with time[2]. Kelvin-Voigt model
The Kelvin-Voigt model, also known as the Voigt model, consists of a Newtonian damper and Hookean elastic spring connected in parallel, as shown in the picture. It is used to explain the stress relaxation behaviors of polymers. The constitutive relation is expressed as a linear first-order differential equation: This model represents a solid undergoing reversible, viscoelastic strain. Upon application of a constant stress, the material deforms at a decreasing rate, asymptotically approaching the steady-state strain. When the stress is released, the material gradually relaxes to its undeformed state. At constant stress (creep), the Model is quite realistic as it predicts strain to tend to σ/E as time continues to infinity. Similar to the Maxwell model, the Kelvin-Voigt Model also has limitations. The model is extremely good with modelling creep in materials, but with regards to relaxation the model is much less accurate. Standard Linear Solid Model
The Standard Linear Solid Model effectively combines the Maxwell Model and a Hookean spring in parallel. A viscous material is modeled as a spring and a dashpot in series with each other, both of which are in parallel with a lone spring. For this model, the governing constitutive relation is: Under a constant stress, the modeled material will instantaneously deform to some strain, which is the elastic portion of the strain, and after that it will continue to deform and asymptotically approach a steady-state strain. This last portion is the viscous part of the strain. Although the Standard Linear Solid Model is more accurate than the Maxwell and Kelvin-Voigt models in predicting material responses, mathematically it returns inaccurate results for strain under specific loading conditions and is rather difficult to calculate. Generalized Maxwell ModelThe Generalized Maxwell also known as the Maxwell-Weichert model (after James Clerk Maxwell and Dieter Weichert) is the most general form of the models described above. It takes into account that relaxation does not occur at a single time, but at a distribution of times. Due to molecular segments of different lengths with shorter ones contributing less than longer ones, there is a varying time distribution. The Weichert model shows this by having as many spring-dashpot Maxwell elements as are necessary to accurately represent the distribution. The Figure on the right represents a possible Weichert model [4]. Effect of temperature on viscoelastic behaviorThe secondary bonds of a polymer constantly break and reform due to thermal motion. Application of a stress favors some conformations over others, so the molecules of the polymer will gradually "flow" into the favored conformations over time. Because thermal motion is one factor contributing to the deformation of polymers, viscoelastic properties change with increasing or decreasing temperature. In most cases, the creep modulus, defined as the ratio of applied stress to the time-dependent strain, decreases with increasing temperature. Generally speaking, an increase in temperature correlates to a logarithmic decrease in the time required to impart equal strain under a constant stress. In other words, it takes less energy to stretch a viscoelastic material an equal distance at a higher temperature than it does at a lower temperature. Viscoelastic creep
When subjected to a step constant stress, viscoelastic materials experience a time-dependent increase in strain. This phenomenon is known as viscoelastic creep. At a time t0, a viscoelastic material is loaded with a constant stress that is maintained for a sufficiently long time period. The material responds to the stress with a strain that increases until the material ultimately fails. When the stress is maintained for a shorter time period, the material undergoes an initial strain until a time t1, after which the strain immediately decreases (discontinuity) then gradually decreases at times t > t1 to a residual strain. Viscoelastic creep data can be presented by plotting the creep modulus (constant applied stress divided by total strain at a particular time) as a function of time [5]. Below its critical stress, the viscoelastic creep modulus is independent of stress applied. A family of curves describing strain versus time response to various applied stress may be represented by a single viscoelastic creep modulus versus time curve if the applied stresses are below the material's critical stress value. Viscoelastic creep is important when considering long-term structural design. Given loading and temperature conditions, designers can choose materials that best suit component lifetimes. Measuring viscoelasticityThough there are many instruments that test the mechanical and viscoelastic response of materials, broadband viscoelastic spectroscopy (BVS) and resonant ultrasound specstroscopy (RUS) are more commonly used to test viscoelastic behavior because they can be used above and below ambient temperatures and are more specific to testing viscoelasticity. These two instruments employ a damping mechanism at various frequencies and time ranges with no appeal to time-temperature superposition [6]. Using BVS and RUS to study the mechanical properties of materials is important to understanding how a material exhibiting viscoelasticity will perform [6]. References
See also
Categories: Continuum mechanics | Materials science | Non-Newtonian fluids | Rubber properties |
|||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Viscoelasticity". A list of authors is available in Wikipedia. |





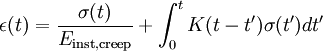
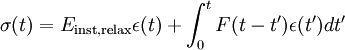
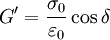
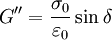
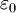 are the amplitudes of stress and strain and
are the amplitudes of stress and strain and 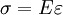
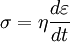
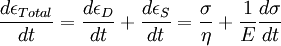 .
.