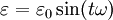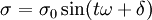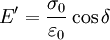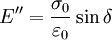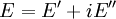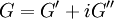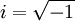My watch list

Dynamic modulus

Dynamic modulus is the ratio of stress to strain under vibratory conditions (calculated from data obtained from either free or forced vibration tests, in shear, compression, or elongation). It is a property of viscoelastic materials.

Additional recommended knowledge

Weighing the right way

Daily Sensitivity Test

Better weighing performance in 6 easy steps

1 Viscoelastic lag
- 1.1 Storage and loss modulus
2 See also
3 References

Viscoelastic lag

Viscoelasticity is studied using the dynamic mechanical analysis. Where we apply small oscillatory strain and measure the resulting stress:

Purely elastic materials have stress and strain in phase, so that the response of one caused by the other is immediate.
In purely viscous materials, strain lags stress by a 90 degree phase lag.
Viscoelastic materials exhibit behavior somewhere in the middle of these two types of material, exhibiting some lag in strain^[1].

Stress and strain in a viscoelastic material can be represented using the following expressions:

Strain: $\varepsilon = \varepsilon_0 \sin(t\omega)$
Stress: $\sigma = \sigma_0 \sin(t\omega + \delta) \,$ ^[1]

where

ω

is period of strain oscillation,

t

is time,

δ

is phase lag between stress and strain.

Storage and loss modulus

The storage and loss modulus in viscoelastic solids measure the stored energy, representing the elastic portion, and the energy dissipated as heat, representing the viscous portion ^[1]. The tensile storage and loss moduli are as follows:

Storage: $E' = \frac {\sigma_0} {\varepsilon_0} \cos \delta$
Loss: $E'' = \frac {\sigma_0} {\varepsilon_0} \sin \delta$ ^[1]