To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Total angular momentum quantum number
In quantum mechanics, the total angular quantum momentum numbers parameterize the total angular momentum of a given particle, by combining its orbital angular momentum and its intrinsic angular momentum (i.e., its spin). Product highlightIf s is the particle's spin angular momentum and l its orbital angular momentum vector, the total angular momentum j is The associated quantum number is the main total angular momentum quantum number j. It can take the following values: where The relation between the total angular momentum vector j and the total angular momentum quantum number j is given by the usual relation (see angular momentum quantum number) the vector's z-projection is given by where mj is the secondary total angular momentum quantum number. It ranges from −j to +j in steps of one. This generates 2j + 1 different values of mj. The total angular momentum corresponds to the Casimir invariant of the Lie algebra SO(3) of the three-dimensional rotation group. See also
References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Total_angular_momentum_quantum_number". A list of authors is available in Wikipedia. |





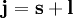
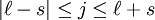
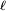 is the
is the