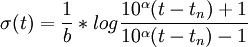Stress relaxation

Stress relaxation describes how polymers relieve stress under constant strain. Because they are viscoelastic, polymers behave in a nonlinear, non-Hookean fashion.^[1] This nonlinearity is described by both stress relaxation and a phenomenon known as creep, which describes how polymers strain under constant stress.

Additional recommended knowledge

Daily Visual Balance Check

What is the Correct Way to Check Repeatability in Balances?

Daily Sensitivity Test

Viscoelastic materials have the properties of both viscous and elastic materials and can be modeled by combining elements that represent these characteristics. One viscoelastic model, called the Maxwell model predicts behavior akin to a spring (elastic element) being in series with a dashpot (viscous element), while the Voigt model places these elements in parallel. Although the Maxwell model is good at predicting stress relaxation, it is fairly poor at predicting creep. On the other hand, the Voigt model is good at predicting creep but rather poor at predicting stress relaxation. The most accurate of the viscoelastic models is the Standard Linear Solid model, which combines the characteristics of both the Maxwell and Voigt models to display both creep and stress relaxation (See Viscoelasticity).^[2]

The following image shows the response of a Standard Linear Solid material to a constant stress, σ₀, over time from t₀ to a later time t_f. For times greater than t_f the load is removed. The curvature of the model represent the effects of both creep and stress relaxation.

E₁ and E₂ refer to the spring constants of the elastic elements of the model.

Stress relaxation calculations can differ for different materials:

To generalize, Obukhov uses power dependencies:^[3]

where σ₀ is the maximum stress at the time the loading was removed (t*), and n is a material parameter.

Vegener et al. use a power series to describe stress relaxation in polyamides:^[3]

To model stress relaxation in glass materials Dowvalter uses the following:^[3]

where α is a material constant and b and t_n depend on processing conditions.

The following non-material parameters all affect stress relaxation in polymers :^[3]

• Magnitude of initial loading
• Speed of loading
• Temperature (isothermal vs non-isothermal conditions)
• Loading medium
• Friction and wear
• Long-term storage

See also

• Creep
• Viscoelasticity
• Standard Linear Solid Model
• Maxwell material
• Kelvin-Voigt material

References