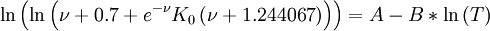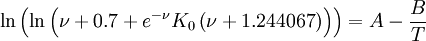To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Temperature dependence of liquid viscosityThe temperature dependence of liquid viscosity is the phenomenon by which liquid viscosity tends to fall (or, alternatively, its fluidity tends to increase) as its temperature increases. This can be observed, for example, by watching how cooking oil appears to move more fluidly upon a frying pan after being heated by a stove. It is usually expressed by one of the following models: Product highlight
Exponential model
where T is temperature and μ0 and b are coefficients. See first-order fluid and second-order fluid. This is an empirical model that usually works for a limited range of temperatures. Arrhenius modelThe model is based on the assumption that the fluid flow obeys the Arrhenius equation for molecular kinetics: where T is temperature, μ0 is a coefficient, E is the activation energy and R is the universal gas constant. A first-order fluid is another name for a power-law fluid with exponential dependence of viscosity on temperature. Williams-Landel-Ferry modelThe Williams-Landel-Ferry model or WLF for short is usually used for polymer melt's or other fluids that have a glass transition temperature. The model is: where T-temperature, C1, C2, Tr and μ0 are empiric parameters (only three of them are independent from each other). If one selects the parameter Tr based on the glass transition temperature, then the parameters C1, C2 become very similar for the wide class of polymers. Typically, if Tr is set to match the glass transition temperature Tg, we get
and
Van Krevelen recommends to choose
and
Using such universal parameters allows one to guess the temperature dependence of a polymer by knowing the viscosity at a single temperature. In reality the universal parameters are not that universal, and it is much better to fit the WLF parameters from the experimental data. Seeton FitThe Seeton Fit is based on curve fitting the viscosity dependence of many liquids (refrigerants, hydrocarbons and lubricants) versus temperature and applies over a large temperature and viscosity range:
Viscosity of water equation accurate to within 2.5% from 0 °C to 370 °C: μ (Temp)= 2.414*10^-5 (N·s/m²) * 10^(247.8 K/(Temp - 140 K))
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Temperature_dependence_of_liquid_viscosity". A list of authors is available in Wikipedia. |





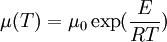
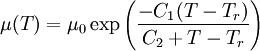
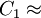 17.44
17.44
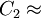 51.6 K.
51.6 K.