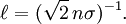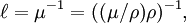To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Mean free pathIn physics the mean free path of a particle, is the average distance the particle travels between collisions with other particles. Product highlight
Derivation
Imagine a beam of particles being shot through a target, and consider an infinitesimally thin slab of the target (Figure 1). The atoms (or particles) that might stop a beam particle are shown in red. The magnitude of mean free path depends on the characteristics of the system the particle is in: Where The area of the slab is L2 and its volume is L2dx. The typical number of stopping atoms in the slab is the concentration n times the volume, i.e., nL2dx. The probability that a beam particle will be stopped in that slab is the net area of the stopping atoms divided by the total area of the slab. where σ is the area (or, more formally, the "scattering cross-section") of one atom. The drop in beam intensity equals the incoming beam intensity multiplied by the probability of being stopped within the slab
This is an ordinary differential equation whose solution is
Thus the expectation value (or average, or simply mean) of x is Fraction of particles that were not stopped (attenuated) by the slab is called transmission Mean free path in kinetic theoryIn kinetic theory mean free path of a particle, such as a molecule, is the average distance the particle travels between collisions with other moving particles. The formula Following table lists some typical values for different pressures.
Mean free path in radiography
In gamma-ray radiography mean free path of a pencil-beam of mono-energetic photons, is the average distance a photon travels between collisions with atoms of the target material. It depends on material and energy of the photons: where μ is linear attenuation coefficient, μ/ρ is mass attenuation coefficient and ρ is density of the material. Mass attenuation coefficient can be looked up or calculated for any material and energy combination using NIST databases [1] [2] In x-ray radiography the calculation of mean free path is more complicated since photons are not mono-energetic, but have some distribution of energies called spectrum. As photons move through the target material they are attenuated with probabilities depending on their energy, as a result their distribution changes in process called Spectrum Hardening. Because of Spectrum Hardening mean free path of x-ray spectrum changes with distance. Sometimes people measure thickness of material in number of mean free paths. Material with thickness of one mean free path will attenuate 37% (1/e) of photons. Standard x-ray image is a transmission image, a minus log of it is sometimes referred as number of mean free paths image. ExamplesA classic application of mean free path is to estimate the size of atoms or molecules. Another important application is in estimating the resistivity of a material from the mean free path of its electrons. For example, for sound waves in an enclosure, the mean free path is the average distance the wave travels between reflections off the enclosure's walls. See also
References
|
|||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Mean_free_path". A list of authors is available in Wikipedia. |





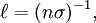
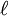 is the mean free path, n is the number of particles per unit volume, and σ is the effective
is the mean free path, n is the number of particles per unit volume, and σ is the effective 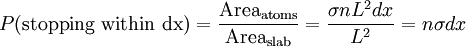
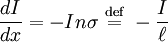
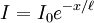 ,
where
,
where 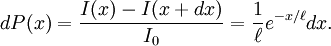
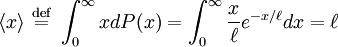
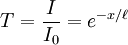 where x is equal to the thickness of the slab
where x is equal to the thickness of the slab