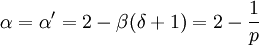To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Widom scalingWidom scaling is a hypothesis in Statistical mechanics regarding the free energy of a magnetic system near its critical point which leads to the critical exponents becoming no longer independent so that they can be paramaterized in terms of two values. Product highlightDefinitionsThe critical exponents α,α',β,γ,γ' and δ are defined in terms of the behaviour of the order parameters and response functions near the critical point as follows
where
DerivationThe scaling hypothesis is that near the critical point, the free energy f(t,H) can be written as the sum of a slowly varying regular part fr and a singular part fs, with the singular part being a scaling function, ie, a homogeneous function, so that
Then taking the partial derivative with respect to H and the form of M(t,H) gives
Setting H = 0 and λ = ( − t) − 1 / p in the preceding equation yields
Comparing this with the definition of β yields its value, Similarly, putting t = 0 and λ = H − 1 / q into the scaling relation for M yields Applying the expression for the isothermal susceptibility χT in terms of M to the scaling relation yields
Setting H=0 and λ = (t) − 1 / p for Similarly for the expression for specific heat cH in terms of M to the scaling relation yields
Taking H=0 and λ = (t) − 1 / p for As a consequence of Widom scaling, not all critical exponents are independent but they can be parameterized by two numbers
The relations are experimentally well verified for magnetic systems and fluids. ReferencesH.E. Stanley, Introduction to Phase Transitions and Critical Phenomena |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Widom_scaling". A list of authors is available in Wikipedia. |





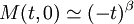 , for
, for 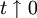
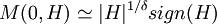 , for
, for 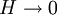
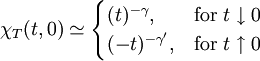
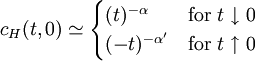
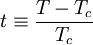 measures the temperature relative to the critical point.
measures the temperature relative to the critical point.
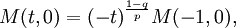 for
for 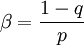
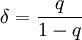
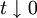 (resp.
(resp. 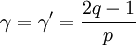
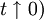 yields
yields
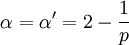
 with the relations expressed as
with the relations expressed as