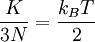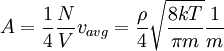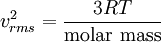To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Kinetic theoryKinetic theory or kinetic theory of gases attempts to explain macroscopic properties of gases, such as pressure, temperature, or volume, by considering their molecular composition and motion. Essentially, the theory posits that pressure is due not to static repulsion between molecules, as was Isaac Newton's conjecture, but due to collisions between molecules moving at different velocities. Kinetic theory is also known as kinetic-molecular theory or collision theory. Product highlight
HistoryIn 1738, Dutch born Swiss physicist and mathematician Daniel Bernoulli published Hydrodynamica, which laid the basis for the kinetic theory of gases. In this work, Bernoulli positioned the argument, still used to this day, that gases consist of great numbers of molecules moving in all directions, that their impact on a surface causes the gas pressure that we feel, and that what we experience as heat is simply the kinetic energy of their motion. The theory was not immediately accepted, in part because conservation of energy had not yet been established, and it was not obvious to physicists how the collisions between molecules could be perfectly elastic. Other pioneers of the kinetic theory were Mikhail Lomonosov (1747), Georges-Louis Le Sage (1818), John Herapath (1820) and John James Waterston (1843), which connected their research with the development of mechanical explanations of gravitation. However, those scientists were neglected by their contemporaries. For example, Herapath, considered how a system of colliding particles could give rise to action at a distance. In this direction, when thinking about the effect of the high temperatures near the Sun on his gravific particles he was led to a relationship between temperature and particle velocity. Herapath postulated that the momentum of a particle in a gases is a measure of the absolute temperature of the gas. He used momentum, rather than the kinetic energy on which the later established theory is based, as it seemed to him to avoid some difficulties around whether elastic collisions were possible between indivisible atoms. Apparently ignorant of Daniel Bernoulli's work, he was led to the incorrect, but suggestive, relationship that expresses the product of pressure P and volume V as proportional to the square of his true temperature. The correct relationship is proportional to the absolute temperature, not its square, the error arising from his identification of momentum, rather than energy, with temperature. In 1859, after reading a paper on the diffusion of molecules by Rudolf Clausius, Scottish mathematical physicist James Clerk Maxwell formulated the Maxwell distribution of molecular velocities, which gave the proportion of molecules having a certain velocity in a specific range. This was the first-ever statistical law in physics.[1] In his 1875 thirteen page article 'Molecules', published in the September issue of Nature, Maxwell states: “we are told that an 'atom' is a material point, invested and surrounded by 'potential forces' and that when 'flying molecules' strike against a solid body in constant succession it causes what is called pressure of air and other gases.”[2] In the beginning of twentieth century, however, atoms were considered by many physicists to be purely hypothetical constructs, rather than real objects. An important turning point was Albert Einstein's 1905 paper on Brownian motion, which succeeded in making certain accurate quantitative predictions based on the kinetic theory. PostulatesThe theory for ideal gases makes the following assumptions:
In addition, if the gas is in a container, the collisions with the walls are assumed to be instantaneous and elastic. More modern developments relax these assumptions and are based on the Boltzmann equation. These can accurately describe the properties of dense gases, because they include the volume of the molecules. The necessary assumptions are the absence of quantum effects, molecular chaos and small gradients in bulk properties. Expansions to higher orders in the density are known as virial expansions. The definitive work is the book by Chapman and Enskog but there have been many modern developments and there is an alternative approach developed by Grad based on moment expansions.[citation needed] In the other limit, for extremely rarefied gases, the gradients in bulk properties are not small compared to the mean free paths. This is known as the Knudsen regime and expansions can be performed in the Knudsen number. The kinetic theory has also been extended to include inelastic collisions in granular matter by Jenkins and others.[citation needed] PressurePressure is explained by kinetic theory as arising from the force exerted by gas molecules impacting on the walls of the container. Consider a gas of N molecules, each of mass m, enclosed in a cuboidal container of volume V. When a gas molecule collides with the wall of the container perpendicular to the x coordinate axis and bounces off in the opposite direction with the same speed (an elastic collision), then the momentum lost by the particle and gained by the wall is: where vx is the x-component of the initial velocity of the particle. The particle impacts the wall once every 2l/vx time units (where l is the length of the container). Although the particle impacts a side wall once every 1l/vx time units, only the momentum change on one wall is considered so that the particle produces a momentum change on a particular wall once every 2l/vx time units. The force due to this particle is: The total force acting on the wall is: where the summation is over all the gas molecules in the container. The magnitude of the velocity for each particle will follow: Now considering the total force acting on all six walls, adding the contributions from each direction we have: where the factor of two arises from now considering both walls in a given direction. Assuming there are a large number of particles moving sufficiently randomly, the force on each of the walls will be approximately the same and now considering the force on only one wall we have: The quantity Thus the force can be written as: Pressure, which is force per unit area, of the gas can then be written as: where A is the area of the wall of which the force exerted on is considered. Thus, as cross-sectional area multiplied by length is equal to volume, we have the following expression for the pressure where V is the volume. Also, as Nm is the total mass of the gas, and mass divided by volume is density where ρ is the density of the gas. This result is interesting and significant, because it relates pressure, a macroscopic property, to the average (translational) kinetic energy per molecule (1/2mvrms2), which is a microscopic property. Note that the product of pressure and volume is simply two thirds of the total kinetic energy. Temperature and kinetic energyFrom the ideal gas law,
where
and the kinetic energy
Eq.(3)1 is one important result of the kinetic theory: The average molecular kinetic energy is proportional to the absolute temperature. From Eq.(1) and Eq.(3)1, we have
Thus, the product of pressure and volume per mole is proportional to the average (translational) molecular kinetic energy. Eq.(1) and Eq.(4) are called the "classical results", which could also be derived from statistical mechanics. Since there are
In the kinetic energy per dof, the constant of proportionality of temperature is 1/2 times Boltzmann constant. This result is related to the equipartition theorem. As noted in the article on heat capacity, diatomic gases should have 7 degrees of freedom, but the lighter gases act as if they have only 5. Thus the kinetic energy per kelvin (monatomic ideal gas) is:
At standard temperature (273.15 K), we get:
Number of collisions with wallOne can calculate the number of atomic or molecular collisions with a wall of a container per unit area per unit time. Assuming an ideal gas, a derivation[3] results in an equation for total number of collisions per unit time per area: RMS speeds of moleculesFrom the kinetic energy formula it can be shown that with v in m/s, T in kelvins, and R is the gas constant. The molar mass is given as kg/mol. The most probable speed is 81.6% of the rms speed, and the mean speeds 92.1% (distribution of speeds). See alsoReferencesThe Mathematical Theory of Non-uniform Gases : An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases Sydney Chapman, T. G. Cowling Categories: Gases | Thermodynamics |
|||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Kinetic_theory". A list of authors is available in Wikipedia. |





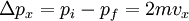
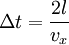
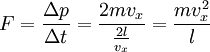
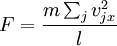
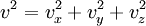
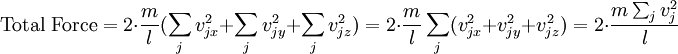
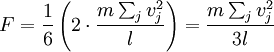
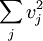 can be written as
can be written as 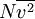 , where the bar denotes an average, in this case an average over all particles. This quantity is also denoted by
, where the bar denotes an average, in this case an average over all particles. This quantity is also denoted by 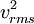 where
where 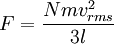
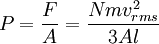
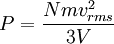
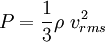
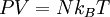
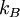 is the
is the
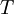 the
the
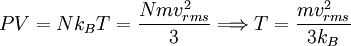
 of the system can now written as
of the system can now written as
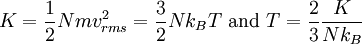
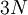 degrees of freedom
(dofs)
in a monoatomic-gas system with
degrees of freedom
(dofs)
in a monoatomic-gas system with
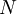 particles,
the kinetic energy per dof is
particles,
the kinetic energy per dof is