To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Gibbs paradox
Originally considered by Josiah Willard Gibbs in his paper On the Equilibrium of Heterogeneous Substances, [1] [2] the Gibbs paradox (Gibbs' paradox or Gibbs's paradox) applies to thermodynamics. It involves the discontinuous nature of the entropy of mixing. This discontinuous nature is paradoxical to the continuous nature of entropy itself with respect to equilibrium and irreversibility in thermodynamic systems. Suppose we have a box divided in half by a movable partition. On one side of the box is an ideal gas A, and on the other side is an ideal gas B at the same temperature and pressure. When the partition is removed, the two gases mix, and the entropy of the system increases because there is a larger degree of uncertainty in the position of the particles. It can be shown that the entropy of mixing multiplied by the temperature is equal to the amount of work one must do in order to restore the original conditions: gas A on one side, gas B on the other. If the gases are the same, no work is needed, but given a tiniest difference between the two, the work needed jumps to a large value, and furthermore it is the same value as when the difference between the two gases is great. Entropy of mixing of liquids, solids and solutions can be calculated in a similar fashion and Gibbs paradox can be applied to liquids, solids and solutions in condensed phases as well as the gaseous phase. Product highlight
Similarity and entropy of mixingWhen Gibbs paradox is discussed, the correlation of the entropy of mixing with similarity is always very controversial and there are three very different opinions regarding the entropy value as related to the similarity (Figures a, b and c). Similarity may change continuously: similarity Z=0 if the components are distinguishable; similarity Z=1 if the parts are indistinguishable. Entropy of mixing does not change continuously in the Gibbs paradox.
There are many claimed resolutions [3] and all of them fall into one of these three kinds of entropy of mixing-similarity relationship (Figures a, b and c). A resolution corresponding to Figure (a) consists of accepting the discontinuity as fact, and stating that the common sense and intuitive objections to it are unfounded. This is the resolution given by Gibbs, and clarified by Jaynes[4]. John von Neumann provided an alternative resolution of the Gibbs paradox by removing the discontinuity of the entropy of mixing: it decreases continuously with the increase in the property similarity of the individual components (See Figure b). More recently Shu-Kun Lin provided still another relationship (See Figure c). They will be explained in detail in a following section. Entropy discontinuityClassical explanation in thermodynamicsGibbs himself posed a solution to the problem which many scientists take as Gibbs's own resolution of the Gibbs paradox.[4][5] The crux of his resolution is the fact that if one develops a classical theory based on the idea that the two different types of gas are indistinguishable, and one never carries out any measurement which reveals the difference, then the theory will have no internal inconsistencies. In other words, if we have two gases A and B and we have not yet discovered that they are different, then assuming they are the same will cause us no theoretical problems. If ever we perform an experiment with these gases that yields incorrect results, we will certainly have discovered a method of detecting their difference. This insight suggests that the concept of thermodynamic state and entropy are somewhat subjective. The increase in entropy as a result of mixing multiplied by the temperature is equal to the minimum amount of work we must do to restore the gases to their original separated state. Suppose that the two different gases are separated by a partition, but that we cannot detect the difference between them. We remove the partition. How much work does it take to restore the original thermodynamic state? None—simply reinsert the partition. The fact that the different gases have mixed does not yield a detectable change in the state of the gas, if by state we mean a unique set of values for all parameters that we have available to us to distinguish states. The minute we become able to distinguish the difference, at that moment the amount of work necessary to recover the original macroscopic configuration becomes non-zero, and the amount of work does not depend on the magnitude of the difference. The paradox is resolved by arguing that the discontinuity is real, and that any "common sense" or "intuitive" objection to it is unfounded. Explanation in statistical mechanics and quantum mechanics, N! and entropy extensivityA large number of scientists believe that this paradox is resolved in statistical mechanics (attributed also to Gibbs[6]) or in quantum mechanics by realizing that if the two gases are composed of indistinguishable particles, they obey different statistics than if they are distinguishable. Since the distinction between the particles is discontinuous, so is the entropy of mixing. The resulting equation for the entropy of a classical ideal gas is extensive, and is known as the Sackur-Tetrode equation. The state an ideal gas of energy U, volume V and with N particles, each particle having mass m, is represented by specifying the momentum vector p and the position vector x for each particle. This can be thought of as specifying a point in a 6N-dimensional phase space, where each of the axes corresponds to one of the momentum or position coordinates of one of the particles. The set of points in phase space that the gas could occupy is specified by the constraint that the gas will have a particular energy: and be contained inside of the volume V (let's say V is a box of side X so that X³=V): for i=1..N and j=1..3. The first constraint defines the surface of a 3N-dimensional hypersphere of radius (2mU)1/2 and the second is a 3N-dimensional hypercube of volume VN. These combine to form a 6N-dimensional hypercylinder. Just as the area of the wall of a cylinder is the circumference of the base times the height, so the area φ of the wall of this hypercylinder is: The entropy is proportional to the logarithm of the number of states that the gas could have while satisfying these constraints. Another way of stating Heisenberg's uncertainty principle is to say that we cannot specify a volume in phase space smaller than h3N where h is Planck's constant. The above "area" must really be a shell of a thickness equal to the uncertainty in momentum Δp so we therefore write the entropy as: where the constant of proportionality is k, Boltzmann's constant. We may take the box length X as the uncertainty in position, and from Heisenbergs uncertainty principle, This quantity is not extensive as can be seen by considering two identical volumes with the same particle number and the same energy. Suppose the two volumes are separated by a barrier in the beginning. Removing or reinserting the wall is reversible, but the entropy difference after removing the barrier is which is in contradiction to thermodynamics. This is the Gibbs paradox. It was resolved by J.W. Gibbs himself, by postulating that the gas particles are in fact indistinguishable. This means that all states that differ only by a permutation of particles should be considered as the same point. For example, if we have a 2-particle gas and we specify AB as a state of the gas where the first particle (A) has momentum p1 and the second particle (B) has momentum p2, then this point as well as the BA point where the B particle has momentum p1 and the A particle has momentum p2 should be counted as the same point. It can be seen that for an N-particle gas, there are N! points which are identical in this sense, and so to calculate the volume of phase space occupied by the gas we must divide Equation 1 by N!.[6] This will give for the entropy: which can be easily shown to be extensive. This is the Sackur-Tetrode equation. If this equation is used, the entropy value will have no difference after mixing two parts of the identical gases. See also:[7] Entropy continuity
Whereas many scientists feel comfortable with the entropy discontinuity shown in Figure (a) and satisfied with the classical or the quantum mechanical explanations in thermodynamics or in statistical mechanics, other people admit that Gibbs paradox is a real paradox which should be resolved by showing entropy continuity. A quantum mechanics resolution of Gibbs paradoxNot many scientists have set out to prove that entropy of mixing is actually continuous. In his book Mathematical Foundations of Quantum Mechanics,[8] John von Neumann provided, for the first time, a resolution to the Gibbs paradox by removing the discontinuity of the entropy of mixing: it decreases continuously with the increase in the property similarity of the individual components (See Figure b). On page 370 of the English version of this book,[8] it reads that " ... This clarifies an old paradox of the classical form of thermodynamics, namely the uncomfortable discontinuity in the operation with semi-permeable walls... We now have a continuous transition." A few scientists agree with this resolution, others are still not convinced. An information theory resolution of Gibbs paradoxAnother entropy continuity relation has been proposed by Shu-Kun Lin[3] based on information theory consideration, as shown in Figure (c). A calorimeter might be employed to determine the entropy of mixing and to either verify the proposition of Gibbs paradox or to resolve the Gibbs paradox. Unfortunately it is well-known that none of the typical mixing processes have a detectable amount of heat and work transferred, even though a large amount of heat, up to the value calculated as TΔS (where T is temperature and S is thermodynamic entropy), should have been measured and a large amount of work up to the amount calculated as ΔG (where G is the Gibbs free energy) should have been observed.[9] We may have to, rather reluctantly, accept the simple fact that the (thermodynamic) entropy change of mixing of ideal gases is always zero, whether the gases are different or identical.[10] This may suggest that entropy of mixing have nothing to do with energy (heat TΔS or work ΔG). A mixing process may be a process of information loss which can be pertinently discussed only in the realm of information theory and entropy of mixing is an (information theory) entropy.[11] Instead of calorimeters, chemical sensors or biosensors can be used to assess the information loss during the mixing process. Mixing 1 mole of gas A and 1 mole of a different gas B will have the increase of at most 2 bits of (information theory) entropy if the two parts of the gas container are used to record 2 bits of information. For condensed phases, instead of the word "mixing", the word "merging" can be used for the process of combining several parts of substance originally in several containers. Then, it is always a merging process, whether the substances are very different or very similar or even the same. Conventional way of entropy of mixing calculation would predict that the mixing (or merging) process of different (distinguishable) substances is more spontaneous than the merging process of the same (indistinguishable) substances. However, this contradicts to all the observed facts in the physical world where the merging process of the same (indistinguishable) substances is the most spontaneous one; immediate examples are spontaneous merging of oil droplets in water and spontaneous crystallization where the indistinguishable unite lattice cells ensemble together. More similar substances are more spontaneously miscible. The two liquids methanol and ethanol are miscible because they are very similar. Without exception, all the experimental observations support the entropy-similarity relation given in Figure (c). It follows that the entropy–similarity relation of Gibbs paradox given in Figure (a) is questionable. A significant conclusion is that, at least in the solid state, the entropy of mixing is a negative value for distinguishable solids: mixing different substances will decrease the (information theory) entropy, and the merging of the indistinguishable molecules (from a large number of containers) to form a phase of pure substance has a great increase in (information theory) entropy. Starting from a binary solid mixture, the process of merging 1 mole of molecules A to become one phase and merging of 1 mole of molecules B to form another phase leads to an (information theory) entropy increase of 2×6.022×1023=12.044×1023bits=1.506×1023Bytes, where 6.022×1023 is the Avogadro's number; and there will be at most only 2 bits of information left. References and Notes
Categories: Thermodynamic entropy | Statistical mechanics | Thermodynamics | Particle statistics |
|||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Gibbs_paradox". A list of authors is available in Wikipedia. |





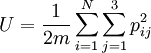
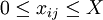
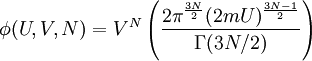
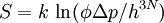
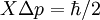 . Solving for
. Solving for ![S = k N \log \left[ V \left(\frac UN \right)^{\frac 32}\right]+ {\frac 32}kN\left( 1+ \log\frac{4\pi m}{3h^2}\right)](images/math/f/3/2/f32e6b968b5b9a18f67e1394d3f01c66.png)
![\delta S = k \left[ 2N \log(2V) - N\log V - N \log V \right] = 2 k N \log 2 > 0](images/math/3/6/a/36a2bf61e69c683b9b514989c41463ca.png)
![S = k N \log \left[ \left(\frac VN\right) \left(\frac UN \right)^{\frac 32}\right]+ {\frac 32}kN\left( {\frac 53}+ \log\frac{4\pi m}{3h^2}\right)](images/math/1/5/c/15c2a150baa131266517c97d54f4d59f.png)


