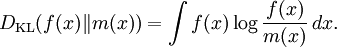To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Information entropy
In information theory, the Shannon entropy or information entropy is a measure of the uncertainty associated with a random variable. It quantifies the information contained in a message, usually in bits or bits/symbol. It is the minimum message length necessary to communicate information. This also represents an absolute limit on the best possible lossless compression of any communication: treating a message as a series of symbols, the shortest number of bits necessary to transmit the message is the Shannon entropy in bits/symbol multiplied by the number of symbols in the original message. A fair coin has an entropy of one bit. However, if the coin is not fair, then the uncertainty is lower (if asked to bet on the next outcome, we would bet preferentially on the most frequent result), and thus the Shannon entropy is lower. A long string of repeating characters has an entropy of 0, since every character is predictable. The entropy of English text is between 1.0 and 1.5 bits per letter.[1] Equivalently, the Shannon entropy is a measure of the average information content the recipient is missing when he does not know the value of the random variable. The concept was introduced by Claude E. Shannon in his 1948 paper "A Mathematical Theory of Communication". DefinitionThe information entropy of a discrete random variable X, that can take on possible values {x1...xn} is where
CharacterizationInformation entropy is characterised by these desiderata: (Define
Any definition of entropy satisfying these assumptions has the form: where K is a constant corresponding to a choice of measurement units. Information entropy explainedFor a random variable
where
To understand the meaning of Eq.(1),
let's first consider a set of
The logarithm is used so to provide the
additivity characteristic for uncertainty.
For example, consider appending to each value of the first
die
the value of a second die, which has
Thus the uncertainty of playing with two dice is obtained by adding
the uncertainty of the second die
Now return to the case of playing with one die only (the first one); we can write In the case of a non-uniform probability mass function (or distribution in the case of continuous random variable), we let
which is also called a surprisal;
the lower the probability
The average uncertainty
and is used as the definition of the information entropy
Example
Consider tossing a coin with known, not necessarily fair, probabilities of coming up heads or tails. The entropy of the unknown result of the next toss of the coin is maximised if the coin is fair (that is, if heads and tails both have equal probability 1/2). This is the situation of maximum uncertainty as it is most difficult to predict the outcome of the next toss; the result of each toss of the coin delivers a full 1 bit of information. However, if we know the coin is not fair, but comes up heads or tails with probabilities p and q, then there is less uncertainty. Every time, one side is more likely to come up than the other. The reduced uncertainty is quantified in a lower entropy: on average each toss of the coin delivers less than a full 1 bit of information. The extreme case is that of a double-headed coin which never comes up tails. Then there is no uncertainty. The entropy is zero: each toss of the coin delivers no information. Further propertiesThe Shannon entropy satisfies the following properties:
This maximal entropy of log2(n) is effectively attained by a source alphabet having a uniform probability distribution: uncertainty is maximal when all possible events are equiprobable. AspectsRelationship to thermodynamic entropyThe inspiration for adopting the word entropy in information theory came from the close resemblance between Shannon's formula and very similar known formulae from thermodynamics. In statistical thermodynamics the most general formula for the thermodynamic entropy S of a thermodynamic system is the Gibbs entropy, defined by J. Willard Gibbs in 1878 after earlier work by Boltzmann (1872).[4] The Gibbs entropy translates over almost unchanged into the world of quantum physics to give the von Neumann entropy, introduced by John von Neumann in 1927, where ρ is the density matrix of the quantum mechanical system. At an everyday practical level the links between information entropy and thermodynamic entropy are not close. Physicists and chemists are apt to be more interested in changes in entropy as a system spontaneously evolves away from its initial conditions, in accordance with the second law of thermodynamics, rather than an unchanging probability distribution. And, as the numerical smallness of Boltzmann's constant kB indicates, the changes in S/kB for even minute amounts of substances in chemical and physical processes represent amounts of entropy which are large right off the scale compared to anything seen in data compression or signal processing. But, at a more philosophical level, connections can be made between thermodynamic and informational entropy, although it took many years in the development of the theories of statistical mechanics and information theory to make the relationship fully apparent. In fact, in the view of Jaynes (1957), thermodynamics should be seen as an application of Shannon's information theory: the thermodynamic entropy is interpreted as being an estimate of the amount of further Shannon information needed to define the detailed microscopic state of the system, that remains uncommunicated by a description solely in terms of the macroscopic variables of classical thermodynamics. For example, adding heat to a system increases its thermodynamic entropy because it increases the number of possible microscopic states that it could be in, thus making any complete state description longer. (See article: maximum entropy thermodynamics). Maxwell's demon can (hypothetically) reduce the thermodynamic entropy of a system by using information about the states of individual molecules; but, as Landauer (from 1961) and co-workers have shown, to function the demon himself must increase thermodynamic entropy in the process, by at least the amount of Shannon information he proposes to first acquire and store; and so the total entropy does not decrease (which resolves the paradox). Entropy as information contentEntropy is defined in the context of a probabilistic model. Independent fair coin flips have an entropy of 1 bit per flip. A source that always generates a long string of A's has an entropy of 0, since the next character will always be an 'A'. The entropy rate of a data source means the average number of bits per symbol needed to encode it. Empirically, it seems that entropy of English text is between .6 and 1.3 bits per character, though clearly that will vary from one source of text to another. Shannon's experiments with human predictors show an information rate of between .6 and 1.3 bits per character, depending on the experimental setup; the PPM compression algorithm can achieve a compression ratio of 1.5 bits per character. From the preceding example, note the following points:
Shannon's definition of entropy, when applied to an information source, can determine the minimum channel capacity required to reliably transmit the source as encoded binary digits. The formula can be derived by calculating the mathematical expectation of the amount of information contained in a digit from the information source. See also Shannon-Hartley theorem. Shannon's entropy measures the information contained in a message as opposed to the portion of the message that is determined (or predictable). Examples of the latter include redundancy in language structure or statistical properties relating to the occurrence frequencies of letter or word pairs, triplets etc. See Markov chain. Data compressionEntropy effectively bounds the performance of the strongest lossless (or nearly lossless) compression possible, which can be realized in theory by using the typical set or in practice using Huffman, Lempel-Ziv or arithmetic coding. The performance of existing data compression algorithms is often used as a rough estimate of the entropy of a block of data. Limitations of entropy as information contentAlthough entropy is often used as a characterization of the information content of a data source, this information content is not absolute: it depends crucially on the probabilistic model. A source that always generates the same symbol has an entropy of 0, but the definition of what a symbol is depends on the alphabet. Consider a source that produces the string ABABABABAB... in which A is always followed by B and vice versa. If the probabilistic model considers individual letters as independent, the entropy rate of the sequence is 1 bit per character. But if the sequence is considered as "AB AB AB AB AB..." with symbols as two-character blocks, then the entropy rate is 0 bits per character. However, if we use very large blocks, then the estimate of per-character entropy rate may become artificially low. This is because in reality, the probability distribution of the sequence is not knowable exactly; it is only an estimate. For example, suppose one considers the text of every book ever published as a sequence, with each symbol being the text of a complete book. If there are N published books, and each book is only published once, the estimate of the probability of each book is 1/N, and the entropy (in bits) is -log2 1/N. As a practical code, this corresponds to assigning each book a unique identifier and using it in place of the text of the book whenever one wants to refer to the book. This is enormously useful for talking about books, but it is not so useful for characterizing the information content of an individual book, or of language in general: it is not possible to reconstruct the book from its identifier without knowing the probability distribution, that is, the complete text of all the books. The key idea is that the complexity of the probabilistic model must be considered. Kolmogorov complexity is a theoretical generalization of this idea that allows the consideration of the information content of a sequence independent of any particular probability model; it considers the shortest program for a universal computer that outputs the sequence. A code that achieves the entropy rate of a sequence for a given model, plus the codebook (i.e. the probabilistic model), is one such program, but it may not be the shortest. Data as a Markov processA common way to define entropy for text is based on the Markov model of text. For an order-0 source (each character is selected independent of the last characters), the binary entropy is: where pi is the probability of i. For a first-order Markov source (one in which the probability of selecting a character is dependent only on the immediately preceding character), the entropy rate is: where i is a state (certain preceding characters) and pi(j) is the probability of j given i as the previous character (s). For a second order Markov source, the entropy rate is b-ary entropyIn general the b-ary entropy of a source Note: the b in "b-ary entropy" is the number of different symbols of the "ideal alphabet" which is being used as the standard yardstick to measure source alphabets. In information theory, two symbols are necessary and sufficient for an alphabet to be able to encode information, therefore the default is to let b = 2 ("binary entropy"). Thus, the entropy of the source alphabet, with its given empiric probability distribution, is a number equal to the number (possibly fractional) of symbols of the "ideal alphabet", with an optimal probability distribution, necessary to encode for each symbol of the source alphabet. Also note that "optimal probability distribution" here means a uniform distribution: a source alphabet with n symbols has the highest possible entropy (for an alphabet with n symbols) when the probability distribution of the alphabet is uniform. This optimal entropy turns out to be EfficiencyA source alphabet encountered in practice should be found to have a probability distribution which is less than optimal. If the source alphabet has n symbols, then it can be compared to an "optimized alphabet" with n symbols, whose probability distribution is uniform. The ratio of the entropy of the source alphabet with the entropy of its optimized version is the efficiency of the source alphabet, which can be expressed as a percentage. This implies that the efficiency of a source alphabet with n symbols can be defined simply as being equal to its n-ary entropy. See also Redundancy (information theory). Extending discrete entropy to the continuous case: differential entropy
The Shannon entropy is restricted to random variables taking discrete values. The formula where f denotes a probability density function on the real line, is analogous to the Shannon entropy and could thus be viewed as an extension of the Shannon entropy to the domain of real numbers. A precursor of the continuous information entropy
Formula (*) is usually referred to as the continuous entropy, or differential entropy. Although the analogy between both functions is suggestive, the following question must be set: is the differential entropy a valid extension of the Shannon discrete entropy? To answer this question, we must establish a connection between the two functions: We wish to obtain a generally finite measure as the bin size goes to zero. In the discrete case, the bin size is the (implicit) width of each of the n (finite or infinite) bins whose probabilities are denoted by pn. As we generalize to the continuous domain, we must make this width explicit. To do this, start with a continuous function f discretized as shown in the figure. As the figure indicates, by the mean-value theorem there exists a value xi in each bin such that and thus the integral of the function f can be approximated (in the Riemannian sense) by where this limit and bin size goes to zero are equivalent. We will denote and expanding the logarithm, we have As and so But note that which is, as said before, referred to as the differential entropy. This means that the differential entropy is not a limit of the Shannon entropy for n → ∞ It turns out as a result that, unlike the Shannon entropy, the differential entropy is not in general a good measure of uncertainty or information. For example, the differential entropy can be negative; also it is not invariant under continuous co-ordinate transformations. Another useful measure of entropy for the continuous case is the relative entropy of a distribution, defined as the Kullback-Leibler divergence from the distribution to a reference measure m(x), The relative entropy carries over directly from discrete to continuous distributions, and is invariant under co-ordinate reparametrisations. References
This article incorporates material from Shannon's entropy on PlanetMath, which is licensed under the GFDL. See also
| ||||||||||||||
| Theory | Entropy · Complexity · Redundancy | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Entropy encoding | Huffman · Adaptive Huffman · Arithmetic (Shannon-Fano · Range) · Golomb · Exp-Golomb · Universal (Elias · Fibonacci) · Asymmetric binary | |||||||||||||
| Dictionary | RLE · LZ77/78 · LZW · LZWL · LZO · DEFLATE · LZMA · LZX | |||||||||||||
| Others | CTW · BWT · PPM · DMC |
| Theory | Convolution · Sampling · Nyquist–Shannon theorem |
|---|---|
| Audio codec parts | LPC (LAR · LSP) · WLPC · CELP · ACELP · A-law · μ-law · MDCT · Fourier transform · Psychoacoustic model |
| Others | Dynamic range compression · Speech compression · Sub-band coding |
| Terms | Color space · Pixel · Chroma subsampling · Compression artifact |
|---|---|
| Methods | RLE · Fractal · Wavelet · SPIHT · DCT · KLT |
| Others | Bit rate · Test images · PSNR quality measure · Quantization |
| Terms | Video Characteristics · Frame · Frame types · Video quality |
|---|---|
| Video codec parts | Motion compensation · DCT · Quantization |
| Others | Video codecs · Rate distortion theory (CBR · ABR · VBR) |





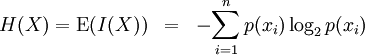
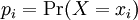 and
and 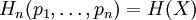 )
)
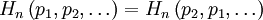 etc.
etc.
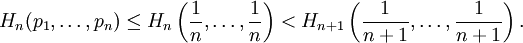
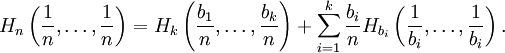
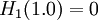
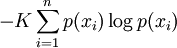
 with
with
 outcomes
outcomes
 ,
the
Shannon information entropy,
a measure of uncertainty (see further below)
and
denoted by
,
the
Shannon information entropy,
a measure of uncertainty (see further below)
and
denoted by
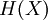 ,
is defined as
,
is defined as
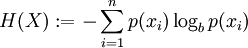
 is the
probability mass function of outcome
is the
probability mass function of outcome
 , and
, and
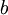 is the base of the logarithm used. Possible values of
is the base of the logarithm used. Possible values of
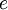 ,
and 10.
The unit of the information entropy
,
and 10.
The unit of the information entropy
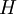 is bit for
is bit for
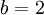 ,
nat for
,
nat for 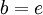 ,
dit (or digit) for
,
dit (or digit) for 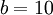 .
.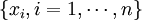 ,
with equal probability
,
with equal probability
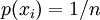 .
An example would be
a fair die
with
.
An example would be
a fair die
with
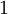 to
to
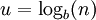
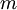 possible
outcomes
possible
outcomes
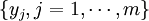 .
There are thus
.
There are thus
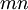 possible outcomes
possible outcomes
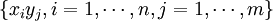 .
The uncertainty for such set of
.
The uncertainty for such set of
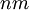 outcomes is then
outcomes is then
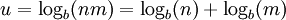
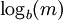 to the uncertainty of the first die
to the uncertainty of the first die
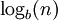 .
.
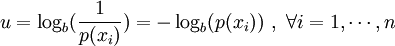
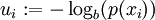
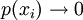 ,
the higher the uncertainty or the surprise, i.e.
,
the higher the uncertainty or the surprise, i.e.
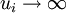 ,
for the outcome
,
for the outcome
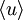 ,
with
,
with
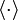 being the average operator,
is obtained by
being the average operator,
is obtained by
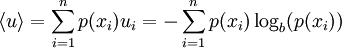
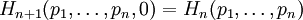 .
.
![H(X) = \operatorname{E}\left[\log_2 \left( \frac{1}{p(X)}\right) \right] = - \operatorname{E}\left[\log_2 \left( p(X)\right) \right] \leq -\log_2 \left( \operatorname{E}\left[ p(X) \right] \right) = \log_2(n)](images/math/2/2/3/223450538414ceb89d9e316dbda90547.png) .
.
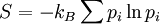
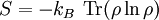
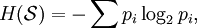
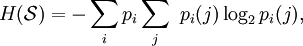
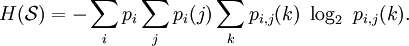
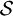 = (S,P) with source alphabet S = {a1, …, an} and discrete probability distribution P = {p1, …, pn} where pi is the probability of ai (say pi = p(ai)) is defined by:
= (S,P) with source alphabet S = {a1, …, an} and discrete probability distribution P = {p1, …, pn} where pi is the probability of ai (say pi = p(ai)) is defined by:
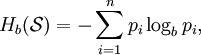
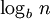 .
.
![h[f] = -\int\limits_{-\infty}^{\infty} f(x) \log f(x)\, dx,\quad (*)](images/math/4/d/c/4dc80af847fc4d2b7ad2cfd27e5a56f1.png)
![\displaystyle h[f]](images/math/6/6/1/6619b4afd2cc8b161c3a1253e664035d.png) given in (*)
is the expression for the functional
given in (*)
is the expression for the functional
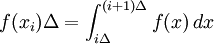
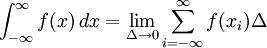
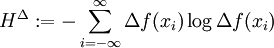
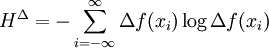
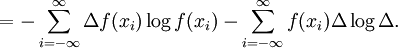
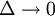 , we have
, we have
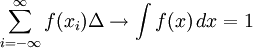
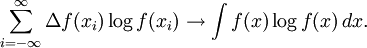
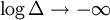 as
as ![h[f] = \lim_{\Delta \to 0} \left[H^{\Delta} + \log \Delta\right] = -\int_{-\infty}^{\infty} f(x) \log f(x)\,dx,](images/math/8/b/e/8bee995e9adc878eb0810576e299b84b.png)