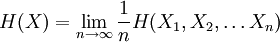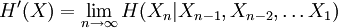My watch list

Entropy rate

The entropy rate of a stochastic process is, informally, the time density of the average information in a stochastic process. For stochastic processes with a countable index, the entropy rate $H (X)$ is the limit of the joint entropy of $n$ members of the process $X k$ divided by $n$ , as $n$ tends to infinity:

$H(X) = \lim_{n \to \infty} \frac{1}{n} H(X_1, X_2, \dots X_n)$

Additional recommended knowledge

What is the Correct Way to Check Repeatability in Balances?

Daily Sensitivity Test

Daily Visual Balance Check

when the limit exists. An alternative, related quantity is:

$H'(X) = \lim_{n \to \infty} H(X_n|X_{n-1}, X_{n-2}, \dots X_1)$

For strongly stationary stochastic processes, $H (X) = H'(X)$ .

Entropy Rates for Markov Chains

Since a stochastic process defined by a Markov chain which is irreducible and aperiodic has a stationary distribution, the entropy rate is independent of the initial distribution.

For example, for such a Markov chain $Y k$ defined on a countable number of states, given the transition matrix $P i j$ , $H (Y)$ is given by:

H(Y) = −	∑	μ_iP_ijlogP_ij
	ij

where $μ i$ is the stationary distribution of the chain.

A simple consequence of this definition is that the entropy rate of an i.i.d. stochastic process has an entropy rate that is the same as the entropy of any individual member of the process.