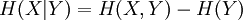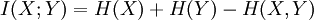To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Joint entropyThe joint entropy is an entropy measure used in information theory. The joint entropy measures how much entropy is contained in a joint system of two random variables. If the random variables are X and Y, the joint entropy is written H(X,Y). Like other entropies, the joint entropy can be measured in bits, nits, or hartleys depending on the base of the logarithm. Product highlight
BackgroundGiven a random variable X, the entropy H(X) describes our uncertainty about the value of X. If X consists of several events x, which each occur with probability px, then the entropy of X is Consider another random variable Y, containing events y occurring with probabilities py. Y has entropy H(Y). However, if X and Y describe related events, the total entropy of the system may not be H(X) + H(Y). For example, imagine we choose an integer between 1 and 8, with equal probability for each integer. Let X represent whether the integer is even, and Y represent whether the integer is prime. One-half of the integers between 1 and 8 are even, and one-half are prime, so H(X) = H(Y) = 1. However, if we know that the integer is even, there is only a 1 in 4 chance that it is also prime; the distributions are related. The total entropy of the system is less than 2 bits. We need a way of measuring the total entropy of both systems. DefinitionWe solve this by considering each pair of possible outcomes (x,y). If each pair of outcomes occurs with probability px,y, the joint entropy is defined as In the example above we are not considering 1 as a prime. Then the joint probability distribution becomes:
Thus, the joint entropy is
PropertiesGreater than subsystem entropiesThe joint entropy is always at least equal to the entropies of the original system; adding a new system can never reduce the available uncertainty. This inequality is an equality if and only if Y is a (deterministic) function of X. if Y is a (deterministic) function of X, we also have
SubadditivityTwo systems, considered together, can never have more entropy than the sum of the entropy in each of them. This is an example of subadditivity. This inequality is an equality if and only if X and Y are statistically independent. BoundsLike other entropies, Relations to Other Entropy MeasuresThe joint entropy is used in the definitions of the conditional entropy: and the mutual information: In quantum information theory, the joint entropy is generalized into the joint quantum entropy. References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Joint_entropy". A list of authors is available in Wikipedia. |





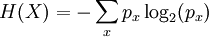
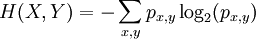
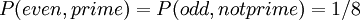
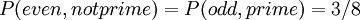
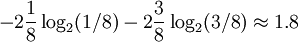 bits.
bits.
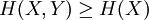
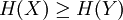
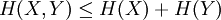
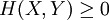 always.
always.