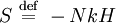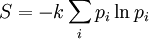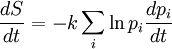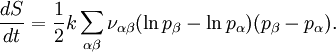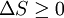To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
H-theoremIn thermodynamics, the H-theorem, introduced by Boltzmann in 1872, describes the increase in the entropy of an ideal gas in an irreversible process, by considering the Boltzmann equation. It appears to predict an irreversible increase in entropy, despite microscopically reversible dynamics. This has led to much discussion. Product highlight
Boltzmann's H-theoremThe quantity H is defined as the integral over velocity space :
where P(v) is the probability. H is a forerunner of Shannon's information entropy. The article on
Shannon's information entropy
contains a
good explanation
of the discrete counterpart of the quantity
Using the Boltzmann equation one can prove that H can only decrease. For a system of N statistically independent particles, H is related to the thermodynamic entropy S through: so, according to the H-theorem, S can only increase. However, Loschmidt objected that it should not be possible to deduce an irreversible process from time-symmetric dynamics and a time-symmetric formalism: something must be wrong (Loschmidt's paradox). The answer is that the theorem is based on Boltzmann's assumption of "molecular chaos", i.e., that it is acceptable for all the particles to be considered independent and uncorrelated. This in fact breaks time reversal symmetry and therefore begs the question. Quantum mechanical H-theoremThe following quantum-mechanical analogue of Boltzmann's H-theorem is sometimes given (e.g., Waldram (1985), p.39). Starting from the Gibbs definition of thermodynamic entropy, differentiating gives (using the fact that ∑ dpi/dt = 0, since ∑ pi = 1). Now Fermi's golden rule gives a master equation for the probability of quantum jumps from state α to β; and from state β to α. For an isolated system the jumps will make a contribution ναβ(pβ-pα) to dpα/dt, and a contribution ναβ(pα-pβ) to dpβ/dt; the micro-reversibility of the dynamics ensuring that the same transition constant ναβ appears in both expressions. Thus But the two brackets will have the same sign, so each contribution to dS/dt cannot be negative. Therefore for an isolated system. The same mathematics is sometimes also presented for classical systems, considering probability flows between coarse-grained cells in the phase space (e.g., Tolman (1938)). CritiqueSeveral criticisms can be made of the above "proof", for example by Gull (1989):
AnalysisAt the heart of the H-theorem is the replacement of 1-state to 1-state deterministic dynamics by many-state to many-state Markovian mixing, with information lost at each Markovian transition. Gull is correct that, with the powers of Laplace's demon, one could in principle map forward exactly the ensemble of the original possible states of the N-particle system exactly, and lose no information. But this would not be very interesting. Part of the program of statistical mechanics, not least the MaxEnt school of which Gull is an enthusiastic proponent, is to see just how much of the detail information in the system one can ignore, and yet still correctly predict experimentally reproducible results. The H-theorem's program of regularly throwing information away, either by systematically ignoring detailed correlations between particles, or between particular sub-systems, or through systematic regular coarse-graining, leads to predictions such as those from the Boltzmann equation for dilute ideal gases or from the recent entropy-production fluctuation theorem, which are useful and reproducibly observable. They also mean that we have learnt something qualitative about the system, and which parts of its information are useful for which purposes, which is additional beyond even the full specification of the microscopic dynamical particle trajectories. (It may be interesting that having rounded on the H-theorem for not considering the microscopic detail of the microscopic dynamics, Gull then chooses to demonstrate the power of the extended-time MaxEnt/Gibbsian method by applying it to a Brownian motion example - a not so dissimilar replacement of detailed deterministic dynamical information by a simplified stochastic/probabilistic summary!) However, it is an assumption that the H-theorem's coarse-graining is not getting rid of any 'interesting' information. With such an assumption, one moves firmly into the domain of predictive physics: if the assumption goes wrong, it may produce predictions which are systematically and reproducibly wrong. See alsoReferences
|
|||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "H-theorem". A list of authors is available in Wikipedia. |





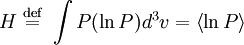
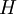 , known as the information entropy or
information uncertainty (with a minus sign).
By
, known as the information entropy or
information uncertainty (with a minus sign).
By