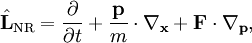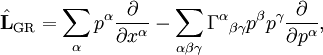To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Boltzmann equation
Product highlightThe Boltzmann equation, also often known as the Boltzmann transport equation, devised by Ludwig Boltzmann, describes the statistical distribution of particles in a fluid. It is one of the most important equations of non-equilibrium statistical mechanics, the area of statistical mechanics that deals with systems far from thermodynamic equilibrium; for instance, when there is an applied temperature gradient or electric field. The Boltzmann equation is used to study how a fluid transports physical quantities such as heat and charge, and thus to derive transport properties such as electrical conductivity, Hall conductivity, viscosity, and thermal conductivity. The Boltzmann equation is an equation for the time t evolution of the distribution (properly a density) function f(x, p, t) in one-particle phase space, where x and p are position and momentum, respectively. The distribution is defined such that
Consider those particles described by f experiencing an external Force F. Then f must satisfy
that is, the particle density in dx dp does not change even though force F is applied and there are no collisions between particles. However, since collisions do occur, the particle density in the phase-space volume dx dp changes. Dividing the equation by dx dp dt and taking the limit, we can get the Boltzmann equation F(x, t) is the force field acting on the particles in the fluid, and m is the mass of the particles. The term on the right hand side is added to describe the effect of collisions between particles; if it is zero then the particles do not collide. The collisionless Boltzmann equation is often mistaken called the Liouville equation (the Liouville Equation is a N-particle Equation). Stosszahl AnsatzThe above Boltzmann equation is of little practical use as it leaves the collision term unspecified. A key insight applied by Boltzmann was to determine the collision term resulting solely from two-body collisions between particles that are assumed to be uncorrelated prior to the collision. This assumption was referred to by Boltzmann as the 'Stosszahl Ansatz', and is also known as the 'molecular chaos assumption'. Under this assumption the collision term can be written as a momentum-space integral over the product of one-particle distribution functions: Extensions and applicationsIt is also possible to write down relativistic Boltzmann equations for systems in which a number of particle species can collide and produce different species. This is how the formation of the light elements in big bang nucleosynthesis is calculated. The Boltzmann equation is also often used in dynamics, especially galactic dynamics. A galaxy, under certain assumptions, may be approximated as a continuous fluid; its mass distribution is then represented by f; in galaxies, physical collisions between the stars are very rare, and the effect of gravitational collisions can be neglected for times far longer than the age of the universe. In Hamiltonian mechanics, the Boltzmann equation is often written more generally as
where L is the Liouville operator describing the evolution of a phase space volume and C is the collision operator. The non-relativistic form of L is and the generalization to (general) relativity is where Γ is the Christoffel symbol. The name Boltzmann equation is also given to this equation: |
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Boltzmann_equation". A list of authors is available in Wikipedia. |





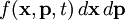 is proportional to the number of particles in the phase-space volume dx dp at time t.
is proportional to the number of particles in the phase-space volume dx dp at time t.
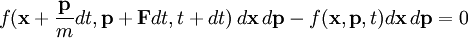 ,
,
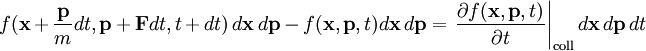
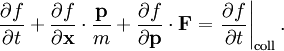
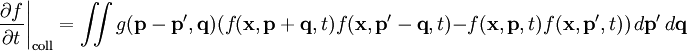
![\hat{\mathbf{L}}[f]=\mathbf{C}[f]](images/math/0/a/a/0aa17ff86ee7d260ba6e1b31172f91d3.png) ,
,