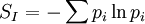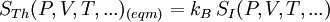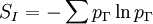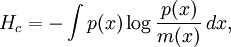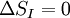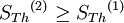Maximum entropy thermodynamics

In physics the Maximum entropy school of thermodynamics (or more colloquially, the MaxEnt school of thermodynamics), initiated with two papers published in the Physical Review by Edwin T. Jaynes in 1957, views statistical mechanics as an inference process: a specific application of inference techniques rooted in information theory, which relate not just to equilibrium thermodynamics, but are general to all problems requiring prediction from incomplete or insufficient data (such as for example image reconstruction, spectral analysis, or inverse problems).

Additional recommended knowledge

Better weighing performance in 6 easy steps

Daily Visual Balance Check

How to quickly check pipettes?

Maximum Shannon entropy

Central to the MaxEnt thesis is the principle of maximum entropy, which states that given certain testable information about a probability distribution, for example particular expectation values, but which is not in itself sufficient to uniquely determine the distribution, one should prefer the distribution which maximises the Shannon information entropy.

This is known as the Gibbs algorithm, having been introduced first by J. Willard Gibbs in 1878, to set up statistical ensembles to predict the properties of thermodynamic systems at equilibrium. It is the cornerstone of the statistical mechanical analysis of the thermodynamic properties of equilibrium systems. (See partition function).

A direct connection is thus made between the equilibrium thermodynamic entropy S_Th, a state function of pressure, volume, temperature, etc., and the information entropy for the predicted distribution with maximum uncertainty conditioned only on the expectation values of those variables:

The presence of k_B, Boltzmann's constant, has no fundamental physical significance here, but is necessary to retain consistency with the previous historical definition of entropy by Clausius (1865). (For further discussion, see Boltzmann's constant).

However, the MaxEnt school argue that the MaxEnt approach is a general technique of statistical inference, with applications far beyond this. It can therefore also be used to predict a distribution for trajectories Γ over a period of time, by maximising:

This information entropy does not necessarily have a simple correspondence with thermodynamic entropy; but it can be used to predict features of non-equilibrium thermodynamic systems as they evolve over time.

In the field of near-equilibrium thermodynamics, the Onsager reciprocal relations and the Green-Kubo relations fall out very directly. The approach also creates a solid theoretical framework for the study of far-from-equilibrium thermodynamics, making the derivation of the entropy production fluctuation theorem particularly straightforward. However, practical calculations for most far-from-equilibrium systems remain very challenging.

(Technical note: for the reasons discussed in the article differential entropy, the simple definition of Shannon entropy ceases to be so directly applicable for probabilities of continuous variables. Instead the appropriate quantity to maximise is the relative information entropy,

the negative of the Kullback-Leibler divergence, or discrimination information, of m(x) from p(x), where m(x) is a prior invariant measure for the variable(s). The relative entropy H_c is always less than zero, and can be thought of as (the negative of) the number of bits of uncertainty lost by fixing on p(x) rather than m(x). Unlike the Shannon entropy, the relative entropy H_c has the advantage of remaining finite and well-defined for continuous x, and invariant under 1-to-1 co-ordinate transformations. The two expressions co-incide for discrete probability distributions, if one can make the assumption that m(x_i) is uniform - i.e. the principle of equal a-priori probability, which underlies statistical thermodynamics).

Philosophical Implications

Adherents to the MaxEnt viewpoint tend to take a very definite position on some of the conceptual/philosophical questions in thermodynamics.

The nature of the probabilities in statistical mechanics

According to the MaxEnt viewpoint, the probabilities in statistical mechanics are subjective (epistemic, personal), to the extent that they are conditioned on a particular model for the underlying state space (e.g. Liouvillian phase space); and they are conditioned on a particular partial description of the system (the macroscopic description of the system used to constrain the MaxEnt probability assignment). The probabilities are objective to the extent that given these inputs, a uniquely defined probability distribution will result.

At a trivial level, the probabilities cannot be entirely objective, because in reality there is only one system, and (assuming determinism) a single unknown trajectory it will evolve through. The probabilities therefore represent a lack of information in the analyst's macroscopic description of the system, not a property of the underlying reality itself.

Moreover, the quality of the predicted probabilities depends on whether the macroscopic model constraints really are a sufficiently accurate and/or complete description of the system to capture all of the experimentally reproducible behaviour. This cannot be guaranteed, a priori. For this reason MaxEnt proponents also call the method predictive statistical mechanics. The predictions can fail. But if they do, this is informative, because it signals the presence of new constraints needed to capture reproducible behaviour in the system, which had not been taken into account.

Is entropy "real" ?

The thermodynamic entropy (at equilibrium) is a function of the state variables of the model description. It is therefore as "real" as the other variables in the model description. If the model constraints in the probability assignment are a "good" description, containing all the information needed to predict reproducible experimental results, then that includes all of the results one could predict using the formulae involving entropy from classical thermodynamics. To that extent, the MaxEnt S_Th is as "real" as the entropy in classical thermodynamics.

Of course in reality there is only one real state of the system. The entropy is not a direct function of that state. It is a function of the real state only through the (subjectively chosen) macroscopic model description.

Is ergodic theory relevant ?

The Gibbsian ensemble idealises the notion of repeating an experiment again and again on different systems, not again and again on the same system. So long-term time averages and the ergodic hypothesis, despite the intense interest in them in the first part of the twentieth century, strictly speaking are not relevant to the probability assignment for the state one might find the system in.

However, this changes if there is additional knowledge that the system is being prepared in a particular way some time before the measurement. One must then consider whether this gives further information which is still relevant at the time of measurement. The question of how 'rapidly mixing' different properties of the system are then becomes very much of interest. Information about some degrees of freedom of the combined system may become unusable very quickly; information about other properties of the system may go on being relevant for a considerable time.

If nothing else, the medium and long-run time correlation properties of the system are interesting subjects for experimentation in themselves. Failure to accurately predict them is a good indicator that relevant macroscopically determinable physics may be missing from the model.

The Second Law

According to Liouville's theorem for Hamiltonian dynamics, the hyper-volume of a cloud of points in phase space remains constant as the system evolves. Therefore, the information entropy must also remain constant, if we condition on the original information, and then follow each of those microstates forward in time:

However, as time evolves, that initial information we had becomes less directly accessible. Instead of being easily summarisable in the macroscopic description of the system, it increasingly relates to very subtle correlations between the positions and momenta of individual molecules. (Compare the discussion of Boltzmann's H-theorem). Equivalently, it means that the probability distribution for the whole system, in 6N-dimensional phase space, becomes increasingly irregular, spreading out into long thin fingers rather than the initial tightly defined volume of possibilities.

Classical thermodynamics is built on the assumption that entropy is a state function of the macroscopic variables -- ie that none of the history of the system matters, it can all be ignored.

The extended, wispy, evolved probability distribution, which still has the initial Shannon entropy S_Th⁽¹⁾, should reproduce the expectation values of the observed macroscopic variables at time t₂. However it will no longer necessarily be a maximum entropy distribution for that new macroscopic description. On the other hand, the new thermodynamic entropy S_Th⁽²⁾ assuredly will measure the maximum entropy distribution, by construction. Therefore, we expect:

This result can be interpreted at different levels. At an abstract level, it means simply that some of the information we originally had about the system has become no longer useful at a macroscopic level. Alternatively, at the level of the 6N-dimensional probability distribution, it represents coarse graining -- ie information loss by smoothing out very fine-scale detail.

Caveats with the argument

Some caveats should be considered with the above.

1. Like all statistical mechanical results according to the MaxEnt school, this increase in thermodynamic entropy is only a prediction. It assumes in particular that the initial macroscopic description contains all of the information relevant to predicting the later macroscopic state. This may not be the case, for example if the initial description fails to reflect some aspect of the preparation of the system which later becomes relevant. In that case the failure of a MaxEnt prediction tells us that there is something more which is relevant that we may have overlooked in the physics of the system.

It is also sometimes suggested that quantum measurement, especially in the decoherence interpretation, may give an apparently unexpected reduction in entropy per this argument, as it appears to involve macroscopic information becoming available which was previously inaccessible. (However, the entropy accounting of quantum measurement is tricky, because to get full decoherence one may be assuming an infinite environment, with an infinite entropy).

2. The argument so far has glossed over the question of fluctuations. It has also implicitly assumed that the uncertainty predicted at time t₁ for the variables at time t₂ will be much smaller than the measurement error. But if the measurements do meaningfully update our knowledge of the system, our uncertainty as to its state is reduced, giving a new S_I⁽²⁾ which is less than S_I⁽¹⁾. (Note that if we allow ourselves the abilities of Laplace's demon, the consequences of this new information can also be mapped backwards, so our uncertainty about the dynamical state at time t₁ is now also reduced from S_I⁽¹⁾ to S_I⁽²⁾ ).

We know that S_Th⁽²⁾ > S_I⁽²⁾; but we can now no longer be certain that it is greater than S_Th⁽¹⁾ = S_I⁽¹⁾. This then leaves open the possibility for fluctuations in S_Th. The thermodynamic entropy may go down as well as up. A more sophisticated analysis is given by the entropy Fluctuation Theorem, which can be established as a consequence of the time-dependent MaxEnt picture.

3. As just indicated, the MaxEnt inference runs equally well in reverse. So given a particular final state, we can ask, what can we retrodict to improve our knowledge about earlier states? However the Second Law argument above also runs in reverse: given macroscopic information at time t₂, we should expect it too to become less useful. The two procedures are time-symmetric. But now the information will become less and less useful at earlier and earlier times. (Compare Loschmidt's paradox). The MaxEnt inference would predict that the most probable origin of a currently low-entropy state would be as a spontaneous fluctuation from an earlier high entropy state. But this conflicts with what we know to have happened, namely that entropy has been increasing steadily, even back in the past.

The MaxEnt proponents' response to this would be that such a systematic failing in the prediction of a MaxEnt inference is a good thing. It means that there is thus clear evidence that some important physical information has been missed in the specification the problem. If it is correct that the dynamics are time-symmetric, it appears that we need to put in by hand a prior probability that initial configurations with a low thermodynamic entropy are more likely than initial configurations with a high thermodynamic entropy. This cannot be explained by the immediate dynamics. Quite possibly it arises as a reflection of the evident time-asymmetric evolution of the universe on a cosmological scale. (See article: Arrow of time).

References

• E.T. Jaynes, Where do we stand on maximum entropy? in: R. Levine, M. Tribus (Eds.), The Maximum Entropy Formalism, MIT Press, Cambridge, MA (1979). ISBN 0-262-12080-1.
• Extensive archive of further papers by E.T. Jaynes on probability and physics. Many are collected in R.D. Rosenkrantz (Ed.), E.T. Jaynes - Papers on probability, statistics and statistical physics, D. Reidel, Dordrecht, (1983) ISBN 90-277-1448-7
• S.F. Gull, Some misconceptions about entropy in: B. Buck, V. A. Macaulay (Eds.), Maximum Entropy in Action, OUP, Oxford (1991). ISBN 0-19-853963-0.
• Jochen Rau, Statistical Mechanics in a Nutshell lecture notes (1998)
• W.T. Grandy, Foundations of Statistical Mechanics vol 1: Equilibrium Theory; vol 2: Nonequilibrium Phenomena, D. Reidel, Dordrecht, (1987) ISBN 90-277-2489-X, (1988) ISBN 90-277-2649-3.
• W.T. Grandy, Three papers in nonequilibrium statistical mechanics, Found.Phys. 34, 1 (2004); Found.Phys. 34, 21 (2004); Found.Phys. 34, 771 (2004)
• R. Lorenz, Full steam ahead - probably, Science 299, 837-838 (2003)
• R.C. Dewar, Information theory explanation of the fluctuation theorem, maximum entropy production and self-organized criticality in non-equilibrium stationary states, J. Phys. A: Math.Gen., 36 631-641 (2003)
• R.C. Dewar, Maximum entropy production and the fluctuation theorem, J. Phys. A: Math.Gen., 38 L371-L381 (2005)
• G. Grinstein and R. Linsker, Comments on a derivation and application of the 'maximum entropy production' principle, J. Phys. A: Math. Theor., 40 9717-9720 (2007). Shows invalidity of Dewar's derivations (a) of maximum entropy production (MaxEP) from fluctuation theorem for far-from-equilibrium systems, and (b) of a claimed link between MaxEP and self-organized criticality.