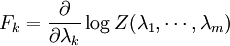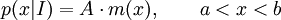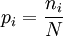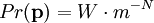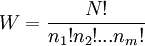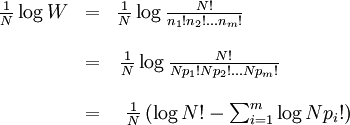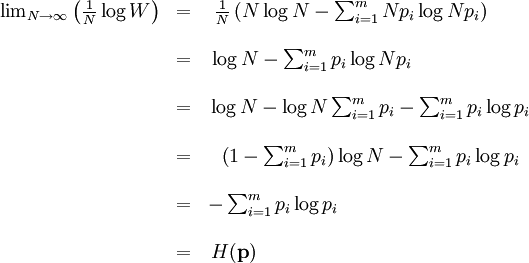To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Principle of maximum entropyThe principle of maximum entropy is a method for analyzing available qualitative information in order to determine a unique epistemic probability distribution. It states that the least biased distribution that encodes certain given information is that which maximizes the information entropy. The principle was first expounded by E.T. Jaynes in 1957 when he introduced what is now known as Maximum entropy thermodynamics: an interpretation of the Gibbs algorithm of statistical mechanics. He suggested that thermodynamics, and in particular thermodynamic entropy, should be seen just as a particular application of a general tool of inference and information theory. The maximum entropy principle is like other Bayesian methods in that it makes explicit use of prior information. This is an alternative to the methods of inference of classical statistics. Product highlight
Testable informationThe principle of maximum entropy is useful only when applied to testable information. A piece of information is testable if it can be determined whether a given distribution is consistent with it. For example, the statements
and
are statements of testable information. Given testable information, the maximum entropy procedure consists of seeking the probability distribution which maximizes information entropy, subject to the constraints of the information. This constrained optimization problem is typically solved using the method of Lagrange multipliers. Entropy maximization with no testable information takes place under a single constraint: the sum of the probabilities must be one. Under this constraint, the maximum entropy probability distribution is the uniform distribution, The principle of maximum entropy can thus be seen as a generalization of the classical principle of indifference, also known as the principle of insufficient reason. General solution for the maximum entropy distribution with linear constraintsDiscrete caseWe have some testable information I about a quantity x ∈ {x1, x2,..., xn}. We express this information as m constraints on the expectations of the functions fk; that is, we require our epistemic probability distribution to satisfy Furthermore, the probabilities must sum to one, giving the constraint The probability distribution with maximum information entropy subject to these constraints is with normalization constant determined by (Interestingly, the Pitman-Koopman theorem states that the necessary and sufficient condition for a sampling distribution to admit sufficient statistics of bounded dimension is that it have the general form of a maximum entropy distribution.) The λk parameters are Lagrange multipliers whose particular values are determined by the constraints according to These m simultaneous equations do not generally possess a closed form solution, and are usually solved by numerical methods. Continuous caseFor continuous distributions, the simple definition of Shannon entropy ceases to be so useful (see differential entropy). Instead what is more useful is the relative entropy of the distribution, (Jaynes, 1963, 1968, 2003), where m(x), which Jaynes called the "invariant measure", is proportional to the limiting density of discrete points. For now, we shall assume that it is known; we will discuss it further after the solution equations are given. Relative entropy is usually defined as the Kullback-Leibler divergence of m from p (although it is sometimes, confusingly, defined as the negative of this). The inference principle of minimizing this, due to Kullback, is known as the Principle of Minimum Discrimination Information. We have some testable information I about a quantity x which takes values in some interval of the real numbers (all integrals below are over this interval). We express this information as m constraints on the expectations of the functions fk, i.e. we require our epistemic probability density function to satisfy And of course, the probability density must integrate to one, giving the constraint The probability density function with maximum Hc subject to these constraints is with normalization constant determined by As in the discrete case, the values of the λk parameters are determined by the constraints according to The invariant measure function m(x) can be best understood by supposing that x is known to take values only in the bounded interval (a, b), and that no other information is given. Then the maximum entropy probability density function is where A is a normalization constant. The invariant measure function is actually the prior density function encoding 'lack of relevant information'. It cannot be determined by the principle of maximum entropy, and must be determined by some other logical method, such as the principle of transformation groups or marginalization theory. Refer to Cover and Thomas for excellent explanation of the ideas . ExamplesFor several examples of maximum entropy distributions, see the article on maximum entropy probability distributions. Justifications for the principle of maximum entropyProponents of the principle of maximum entropy justify its use in assigning epistemic probabilities in several ways, including the following two arguments. These arguments take the use of epistemic probability as given, and thus have no force if the concept of epistemic probability is itself under question. Information entropy as a measure of 'uninformativeness'Consider a discrete epistemic probability distribution among m mutually exclusive propositions. The most informative distribution would occur when one of the propositions was known to be true. In that case, the information entropy would be equal to zero. The least informative distribution would occur when there is no reason to favor any one of the propositions over the others. In that case, the only reasonable probability distribution would be uniform, and then the information entropy would be equal to its maximum possible value, log m. The information entropy can therefore be seen as a numerical measure which describes how uninformative a particular probability distribution is from zero (completely informative) to log m (completely uninformative). By choosing to use the distribution with the maximum entropy allowed by our information, the argument goes, we are choosing the most uninformative distribution possible. To choose a distribution with lower entropy would be to assume information we do not possess; to choose one with a higher entropy would violate the constraints of the information we do possess. Thus the maximum entropy distribution is the only reasonable distribution. The Wallis derivationThe following argument is the result of a suggestion made by Graham Wallis to E. T. Jaynes in 1962 (Jaynes, 2003). It is essentially the same mathematical argument used for the Maxwell-Boltzmann statistics in statistical mechanics, although the conceptual emphasis is quite different. It has the advantage of being strictly combinatorial in nature, making no reference to information entropy as a measure of 'uncertainty', 'uninformativeness', or any other imprecisely defined concept. The information entropy function is not assumed a priori, but rather is found in the course of the argument; and the argument leads naturally to the procedure of maximizing the information entropy, rather than treating it in some other way. Suppose an individual wishes to make an epistemic probability assignment among m mutually exclusive propositions. She has some testable information, but is not sure how to go about including this information in her probability assessment. She therefore conceives of the following random experiment. She will distribute N quanta of epistemic probability (each worth 1/N) at random among the m possibilities. (One might imagine that she will throw N balls into m buckets while blindfolded. In order to be as fair as possible, each throw is to be independent of any other, and every bucket is to be the same size.) Once the experiment is done, she will check if the probability assignment thus obtained is consistent with her information. If not, she will reject it and try again. Otherwise, her assessment will be where ni is the number of quanta that were assigned to the ith proposition. Now, in order to reduce the 'graininess' of the epistemic probability assignment, it will be necessary to use quite a large number of quanta of epistemic probability. Rather than actually carry out, and possibly have to repeat, the rather long random experiment, our protagonist decides to simply calculate and use the most probable result. The probability of any particular result is the multinomial distribution, where is sometimes known as the multiplicity of the outcome. The most probable result is the one which maximizes the multiplicity W. Rather than maximizing W directly, our protagonist could equivalently maximize any monotonic increasing function of W. She decides to maximize At this point, in order simplify the expression, our protagonist takes the limit as N → ∞, i.e. as the epistemic probability levels go from grainy discrete values to smooth continuous values. Using Stirling's approximation, she finds All that remains for our protagonist to do is to maximize entropy under the constraints of her testable information. She has found that the maximum entropy distribution is the most probable of all "fair" random epistemic distributions, in the limit as the probability levels go from discrete to continuous. Compatibility with Bayes RuleRecently, it has been shown that Bayes' Rule and the Principle of Maximum Entropy (MaxEnt) are completely compatible and can be seen as special cases of the Method of Maximum (relative) Entropy (ME). This method reproduces every aspect of orthodox Bayesian inference methods. In addition this new method opens the door to tackling problems that could not be addressed by either the MaxEnt or orthodox Bayesian methods individually. See also
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Principle_of_maximum_entropy". A list of authors is available in Wikipedia. |





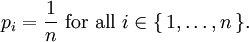
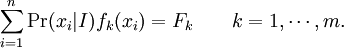
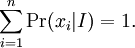
![\Pr(x_i|I) = \frac{1}{Z(\lambda_1,\cdots, \lambda_m)} \exp\left[\lambda_1 f_1(x_i) + \cdots + \lambda_m f_m(x_i)\right]](images/math/5/d/4/5d4ddd7832c285d097285e4efd4a9bf6.png)
![Z(\lambda_1,\cdots, \lambda_m) = \sum_{i=1}^n \exp\left[\lambda_1 f_1(x_i) + \cdots + \lambda_m f_m(x_i)\right].](images/math/9/7/1/9718a9075d2e1029b4c8eb263d07db96.png)
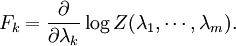
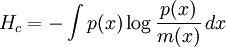
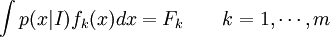
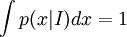
![p(x|I) = \frac{1}{Z(\lambda_1,\cdots, \lambda_m)} m(x)\exp\left[\lambda_1 f_1(x) + \cdots + \lambda_m f_m(x)\right]](images/math/4/d/6/4d680e6dfae786099d35fbf9fb427074.png)
![Z(\lambda_1,\cdots, \lambda_m) = \int m(x)\exp\left[\lambda_1 f_1(x) + \cdots + \lambda_m f_m(x)\right]dx](images/math/4/f/7/4f736ae5513307a663246b8ff218d3fd.png)