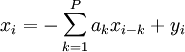To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Maximum entropy spectral estimationThe maximum entropy method applied to spectral density estimation. The overall idea is that the maximum entropy rate stochastic process that satisfies the given constant autocorrelation and variance constraints, is a linear Gauss-Markov process with i.i.d. zero-mean, Gaussian input. Product highlightMethod descriptionThe maximum entropy rate, strongly stationary stochastic process xi with autocorrelation sequence
for arbitrary constants αk is the P-th order, linear Markov chain of the form: where the yi are zero mean, i.i.d. and normally-distributed of finite variance σ2. Spectral estimationGiven the ak, the square of the absolute value of the transfer function of the linear Markov chain model can be evaluated at any required frequency in order to find the power spectrum of xi. References
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Maximum_entropy_spectral_estimation". A list of authors is available in Wikipedia. |





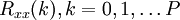 satisfying the constraints:
satisfying the constraints: