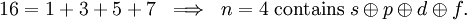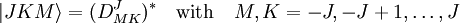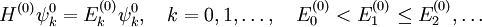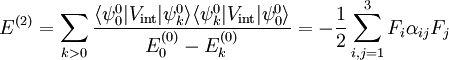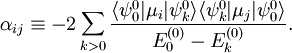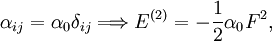To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Stark effectThe Stark effect is the shifting and splitting of spectral lines of atoms and molecules due to the presence of an external static electric field. The amount of splitting and or shifting is called the Stark splitting or Stark shift. In general one distinguishes first- and second-order Stark effects. The first-order effect is linear in the applied electric field, while the second-order effect is quadratic in the field. The Stark effect is responsible for the pressure broadening (Stark broadening) of spectral lines by charged particles. When the split/shifted lines appear in absorption, the effect is called the inverse Stark effect. The Stark effect is the electric analogue of the Zeeman effect where a spectral line is split into several components due to the presence of a magnetic field.
Product highlight
HistoryThe effect is named after Johannes Stark, who discovered it in 1913. It was independently discovered in the same year by the Italian physicist Antonino Lo Surdo, and in Italy it is thus sometimes called the Stark-Lo Surdo effect. The discovery of this effect contributed importantly to the development of quantum theory. Ironically, soon after their discoveries, both Stark and Lo Surdo rejected developments in modern physics and allied themselves with the political and racial programs of Hitler and Mussolini.[1] Inspired by the magnetic Zeeman effect, and especially by Lorentz' explanation of it, Woldemar Voigt[2] performed classical mechanical calculations of quasi-elastically bound electrons in an electric field. By using experimental indices of refraction he gave an estimate of the Stark splittings. This estimate was a few orders of magnitude too low. Not deterred by this prediction, Stark [3] undertook measurements on excited states of the hydrogen atom and succeeded in observing splittings. By the use of the Bohr-Sommerfeld ("old") quantum theory Paul Epstein[4] and Karl Schwarzschild[5] were independently able to derive equations for the linear and quadratic Stark effect in hydrogen. Four years later, Hendrik Kramers[6] derived formulas for intensities of spectral transitions. Kramers also included the effect of "fine structure"—the relativistic increase of electron mass with velocity. (Note that the term "fine structure" no longer refers to relativistic mass effects, but rather to electron spin effects.) The first quantum mechanical treatment (in the framework of Heisenberg's matrix mechanics) was by Wolfgang Pauli[7]. Erwin Schrödinger discussed at length the Stark effect in his third paper[8] on quantum theory (in which he introduced his perturbation theory), once in the manner of the 1916 work of Epstein (but generalized from the old to the new quantum theory) and once by his (first-order) perturbation approach. Finally, Epstein[9] reconsidered the linear and quadratic Stark effect from the point of view of the new quantum theory. He derived equations for the line intensities which were a decided improvement over Kramers' results obtained by the old quantum theory. MechanismClassical electrostaticsThe Stark effect originates from the interaction between a charge distribution (atom or molecule) and an external electric field. Before turning to quantum mechanics we describe the interaction classically and consider a continuous charge distribution ρ(r). If this charge distribution is non-polarizable its interaction energy with an external electrostatic potential V(r) is If the electric field is of macroscopic origin and the charge distribution is microscopic, it is reasonable to assume that the electric field is uniform over the charge distribution. That is, V is given by a two-term Taylor expansion, where we took the origin 0 somewhere within ρ.
With Here we have introduced the dipole moment μ of ρ as an integral over the charge distribution. In case ρ consists of N point charges qj this definition becomes a sum Perturbation theoryTurning now to quantum mechanics we see an atom or a molecule as a collection of point charges (electrons and nuclei), so that the second definition of the dipole applies. The interaction of atom or molecule with a uniform external field is described by the operator This operator is used as a perturbation in first- and second-order perturbation theory to account for the first- and second-order Stark effect. First orderLet the unperturbed atom or molecule be in a g-fold degenerate state with orthonormal zeroth-order state functions If g = 1 (as is often the case for electronic states of molecules) the first-order energy becomes proportional to the expectation (average) value of the dipole operator Because a dipole moment is a polar vector, the diagonal elements of the perturbation matrix Vint vanish for systems with an inversion center (such as atoms). Molecules with an inversion center in a non-degenerate electronic state do not have a (permanent) dipole and hence do not show a linear Stark effect. In order to obtain a non-zero matrix Vint for systems with an inversion center it is necessary that some of the unperturbed functions where The one-electron states with even The first-order Stark effect occurs in rotational transitions of symmetric top molecules (but not for linear and asymmetric molecules). In first approximation a molecule may be seen as a rigid rotor. A symmetric top rigid rotor has the unperturbed eigenstates with 2(2J+1)-fold degenerate energy for |K| > 0 and (2J+1)-fold degenerate energy for K=0. Here DJMK is an element of the Wigner D-matrix. The first-order perturbation matrix on basis of the unperturbed rigid rotor function is non-zero and can be diagonalized. This gives shifts and splittings in the rotational spectrum. Quantitative analysis of these Stark shift yields the permanent electric dipole moment of the symmetric top molecule. Second orderAs stated, the quadratic Stark effect is described by second-order perturbation theory. The zeroth-order problems are assumed to be solved. It is usual to assume that the zeroth-order state to be perturbed is non-degenerate. If we take the ground state as the non-degenerate state under consideration (for hydrogen-like atoms: n = 1), perturbation theory gives with the components of the polarizability tensor α defined by The energy E(2) gives the quadratic Stark effect. Because of their spherical symmetry the polarizability tensor of atoms is isotropic, which is the quadratic Stark shift for atoms. For many molecules this expression is not too bad an approximation, because molecular tensors are often reasonably isotropic. ProblemsThe perturbative treatment of the Stark effect has some problems. In the presence of an electric field, states of atoms and molecules that were previously bound (square-integrable), become formally (non-square-integrable) resonances of finite width. These resonances may decay in finite time via field ionization. For low lying states and not too strong fields the decay times are so long, however, that for all practical purposes the system can be regarded as bound. For highly excited states and very strong fields ionization may have to be accounted for. (See also the article on the Rydberg atom). Quantum-Confined Stark EffectIn a semiconductor heterostructure, where a small bandgap material is sandwiched between two layers of a larger bandgap material, the Stark effect can be dramatically enhanced by bound excitons. This is due to the fact that the electron and hole which form the exciton are pulled in opposite directions by the applied electric field, but they remain confined in the smaller bandgap material, so the exciton is not merely pulled apart by the field. The quantum-confined Stark effect is widely used for semiconductor-based optical modulators, particularly for optical fiber communications. See also
Notes
References
Categories: Atomic physics | Foundational quantum physics |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Stark_effect". A list of authors is available in Wikipedia. |





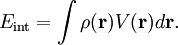

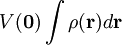 as the zero energy, the interaction becomes
as the zero energy, the interaction becomes
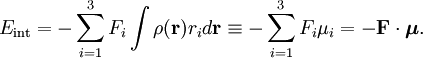
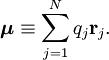
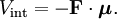
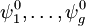 . (Non-degeneracy is the special case g = 1). According to perturbation theory the first-order energies are the eigenvalues of the g x g matrix with general element
. (Non-degeneracy is the special case g = 1). According to perturbation theory the first-order energies are the eigenvalues of the g x g matrix with general element
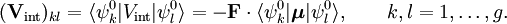
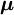 ,
,
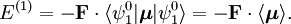
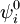 have opposite parity (obtain plus and minus under inversion), because only functions of opposite parity give non-vanishing matrix elements. Degenerate zeroth-order states of opposite parity occur for excited hydrogen-like (one-electron) atoms. Such atoms have the principal quantum number n among their quantum numbers. The excited state of hydrogen-like atoms with principal quantum number n is n2-fold degenerate and
have opposite parity (obtain plus and minus under inversion), because only functions of opposite parity give non-vanishing matrix elements. Degenerate zeroth-order states of opposite parity occur for excited hydrogen-like (one-electron) atoms. Such atoms have the principal quantum number n among their quantum numbers. The excited state of hydrogen-like atoms with principal quantum number n is n2-fold degenerate and
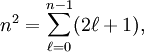
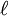 is the azimuthal (angular momentum) quantum number. For instance, the excited n = 4 state contains the following
is the azimuthal (angular momentum) quantum number. For instance, the excited n = 4 state contains the following