To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Rydberg atomA Rydberg atom is an excited atom with one or more electrons that have a very high principal quantum number. These atoms have a number of peculiar properties including an exaggerated response to electric and magnetic fields, long decay periods and electron wavefunctions that approximate under some conditions classical orbits of electrons about the nuclei. In spite of its shortcomings, the Bohr model of the atom is useful in explaining these properties. Classically an electron in a circular orbit of radius where Orbital momentum is quantised in units of Combining these two equations leads to Bohr's expression for the orbital radius in terms of the principal quantum number It is now apparent why Rydberg atoms have such peculiar properties; the radius of the orbit scales as Product highlight
The classical view of Rydberg atomsAn atom in a Rydberg state has a valence electron in a large orbit far from the ion core; in such an orbit the outermost electron feels an almost hydrogenic,
The similarity of the effective potential ‘seen’ by the outer electron to the hydrogen potential is a defining characteristic of Rydberg states and explains why the electron wavefunctions approximate to classical orbits. There are three notable exceptions:
where A & B are constants.
The quantum mechanical picture
Quantum mechanically a state of high This explains why Rydberg states are susceptible to ionisation. The long lifetimes of Rydberg states with high orbital angular momentum can be explained in terms of the overlapping of wavefunctions. The wavefunction of an electron in a high The three exceptions to the definition of a Rydberg atom as an atom with a hydrogenic potential, have an alternative, quantum mechanical explanation:
What makes Rydberg atoms worth studying?Experimental atomic physicsAlthough the interesting nature of Rydberg atoms has been understood since the development of the Bohr model in 1913, for a long time there was no efficient method for producing large, single-state, mono-energetic populations. There were a number of interesting experiments done in the 1950s and 1960s using electron impact excitation: and charge exchange excitation: but these techniques both produce populations with a very broad spread of energies. The arrival of tunable dye lasers in the 1970s allowed a much greater level of control over populations of excited atoms. In optical excitation the incident photon is absorbed by the atom, thus absolutely specifying the energy of the state produced. The precise control over atomic states allowed by optical excitation has played a significant role in advancing our understanding of atomic Rydberg states. Investigating diamagnetic effectsThe large sizes and low binding energies of Rydberg atoms lead to a high magnetic susceptibility Rydberg atoms in plasmasRydberg atoms form commonly in plasmas due to the recombination of electrons and positive ions; low energy recombination results in fairly stable Rydberg atoms, while recombination of electrons and positive ions with high kinetic energy often form autoionising Rydberg states. Rydberg atoms’ large sizes and susceptibility to perturbation and ionisation by electric and magnetic fields, are an important factor determining the properties of plasmas. Condensation of Rydberg atoms forms Rydberg matter. Rydberg atoms in astrophysicsIn the time between the early absorption spectroscopy experiments and the arrival of tunable lasers, interest in Rydberg atoms was kept alive by the realisation that they are common in interstellar space, and as such are an important radiation source for astronomers. The density within interstellar gas clouds is typically many orders of magnitude lower than the best laboratory vacuums attainable on Earth, allowing Rydberg atoms to persist for long periods of time without being ionised by collisions or electric and magnetic fields. As a result of this longevity and the abundance of hydrogen it is particularly common for astronomers to observe radiation from the heavens at a frequency of 2.4 GHz, now known to correspond to the hydrogen
Classical simulation of a Rydberg atomA simple Application of an external electric field (known in atomic physics as a Stark field) changes the geometry of the potential and dramatically changes the behaviour of the electron. A Coulombic potential does not apply any torque as the force is always antiparallel to the position vector (i.e. always pointing along a line running between the electron and the nucleus): With the application of a static electric field, the electron feels a continuously changing torque. The resulting trajectory becomes progressively more distorted over time, eventually going through the full range of angular momentum from
The time period of the oscillation in angular momentum (the time to complete the trajectory in the figure below), almost exactly matches the quantum mechanically predicted period for the wavefunction to return to its initial state, demonstrating the classical nature of the Rydberg atom. See also
References
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Rydberg_atom". A list of authors is available in Wikipedia. |


 , about a
, about a 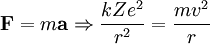
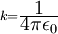 .
.
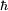 :
:
 :
:
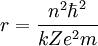
 (the
(the 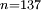 state of hydrogen has an atomic radius ~1µm) and the geometric cross-section as
state of hydrogen has an atomic radius ~1µm) and the geometric cross-section as  . Thus Rydberg atoms are extremely large with loosely bound valence electrons, easily perturbed or
. Thus Rydberg atoms are extremely large with loosely bound valence electrons, easily perturbed or 


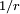 coulomb potential from a compact ion core consisting of a
coulomb potential from a compact ion core consisting of a 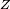
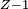 electrons.
electrons.
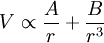
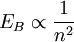
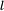 state (high angular momentum, 'circular orbit') has very little overlap with the wavefunctions of the inner electrons and hence remains relatively unperturbed.
state (high angular momentum, 'circular orbit') has very little overlap with the wavefunctions of the inner electrons and hence remains relatively unperturbed.
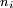 , energetically close to the state of the outer electron
, energetically close to the state of the outer electron 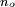 , then its wavefunction become almost as large as the first (a double Rydberg state). This occurs as
, then its wavefunction become almost as large as the first (a double Rydberg state). This occurs as 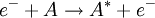
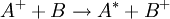
 . As diamagnetic effects scale with the area of the orbit and the area is proportional to the radius squared
. As diamagnetic effects scale with the area of the orbit and the area is proportional to the radius squared 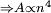 , effects impossible to detect in ground state atoms become obvious in Rydberg atoms, which demonstrate very large diamagnetic shifts.
, effects impossible to detect in ground state atoms become obvious in Rydberg atoms, which demonstrate very large diamagnetic shifts.
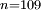 to
to 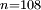 transition. Such a highly excited hydrogen atom on Earth would be ionised almost immediately as the binding energy would be significantly below
transition. Such a highly excited hydrogen atom on Earth would be ionised almost immediately as the binding energy would be significantly below 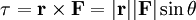
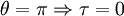
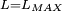 , to a straight line
, to a straight line 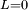 , to the initial orbit in the opposite sense
, to the initial orbit in the opposite sense
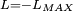 .
.


