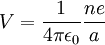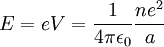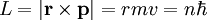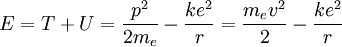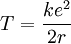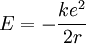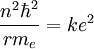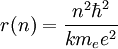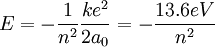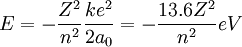To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Ionization potentialThe ionization potential, ionization energy or EI of an atom or molecule is the energy required to remove one mole of electrons from one mole of isolated gaseous atoms or ions. More generally, the nth ionization energy is the energy required to strip it of an nth mole of electrons after the first n − 1 mole of electrons have already been removed. It is considered in physical chemistry as a measure of the "reluctance" of an atom or ion to surrender an electron, or the "strength" by which the electron is bound; the greater the ionization energy, the more difficult it is to remove an electron. The ionization potential is an indicator of the reactivity of an element. Elements with a low ionization energy tend to be reducing agents and to form salts. Product highlight
Values and trends
The next ionization energy involves removing an electron from an orbital closer to the nucleus. Electrons in the closer orbital experience greater forces of electrostatic attraction, and thus, require more energy to be removed. Some values for elements of the third period are given in the following table:
In order to determine how many electrons are in the outermost shell of an element, one can use the ionization energy. If, for example, it required 1,500 kJ/mol to remove one mole of electrons and required 6,000 kJ/mol to remove another mole of electrons and then 5,000 kJ/mol, etc. this means that the element had one electron in its outermost shell. This means that the element is a metal and in order for this element to achieve a stable complete outer shell, it looks to lose one electron. Thus, the first electron is easy to remove and consequently the ionization energy is low. Notice, however, that once the stable complete outer shell has been formed, it becomes much more difficult to remove the next electron. If that electron can be removed the consequent one can be removed a bit more easily. Electrostatic explanationAtomic ionization energy can be predicted by an analysis using electrostatic potential and the Bohr model of the atom, as follows. Consider an electron of charge -e, and an ion with charge +ne, where n is the number of electrons missing from the ion. According to the Bohr model, if the electron were to approach and bind with the atom, it would come to rest at a certain radius a. The electrostatic potential V at distance a from the ionic nucleus, referenced to a point infinitely far away, is:
Since the electron is negatively charged, it is drawn to this positive potential. (The value of this potential is called the ionization potential). The energy required for it to "climb out" and leave the atom is:
This analysis is incomplete, as it leaves the distance a as an unknown variable. It can be made more rigorous by assigning to each electron of every chemical element a characteristic distance, chosen so that this relation agrees with experimental data. It is possible to expand this model considerably by taking a semi-classical approach, in which momentum is quantized. This approach works very well for the hydrogen atom, which only has one electron. The magnitude of the angular momentum for a circular orbit is:
The total energy of the atom is the sum of the kinetic and potential energies, that is:
Velocity can be eliminated from the kinetic energy term by setting the Coulomb attraction equal to the centripetal force, giving:
Now the energy can be found in terms of k, e, and r. Using the new value for the kinetic energy in the total energy equation above, it is found that:
Solving the angular momentum for v and substituting this into the expression for kinetic energy, we have:
This establishes the dependence of the radius on n. That is:
At its smallest value, n is equal to 1 and r is the Bohr radius a0. Now, the equation for the energy can be established in terms of the Bohr radius. Doing so gives the result:
This can be expanded to larger nuclei by incorporating the atomic number into the equation.
Quantum-mechanical explanationAccording to the more sophisticated theory of quantum mechanics, the location of an electron is best described as a "cloud" of likely locations that ranges near and far from the nucleus, or in other words a probability distribution. The energy can be calculated by integrating over this cloud. The cloud's underlying mathematical representation is the wavefunction which is built from a Slater determinant consisting of molecular spin orbitals. These are related by Pauli's exclusion principle to the antisymmetrized products of the atomic or molecular orbitals. This linear combination is called a configuration interaction expansion of the electronic wavefunction. In general, calculating the nth ionization energy requires subtracting the energy of a Z − n + 1 electron system from the energy of a Z − n electron system. Calculating these energies is not simple, but is a well-studied problem and is routinely done in computational chemistry. At the lowest level of approximation, the ionization energy is provided by Koopmans' theorem. See also
Categories: Ions | Molecular physics | Atomic physics | Chemical properties | Quantum chemistry |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Ionization_potential". A list of authors is available in Wikipedia. |