To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Work functionThe work function is the minimum energy (usually measured in electron volts) needed to remove an electron from a solid to a point immediately outside the solid surface (or energy needed to move an electron from the Fermi energy level into vacuum). Here "immediately" means that the final electron position is far from the surface on the atomic scale but still close to the solid on the macroscopic scale. The work function is an important property of metals. The magnitude of the work function is usually about a half of the ionization energy of a free atom of the metal. Product highlight
Work Function and Surface EffectWork function W of a metal is closely related to its Fermi energy level It can be proven that if we define work function as the minimum energy needed to remove an electron to a point immediately out of the solid, the effect of the surface charge distribution can be neglected, leaving only the surface dipole distribution. Let the potential energy difference across the surface due to effective surface dipole be
Where ExampleFor example, Caesium has ionization energy 3.9 eV and work function 1.9 eV. Photoelectric work functionThe work function is the minimum energy that must be given to an electron to liberate it from the surface of a particular metal. In the photoelectric effect if a photon with an energy greater than the work function is incident on a metal photoelectric emission occurs. Any excess energy is given to the electron as kinetic energy. Photoelectric work function is
where h is the Planck's constant and f0 is the minimum (threshold) frequency of the photon required to produce photoelectric emission. When an electron gains energy, it jumps from one energy level to another in "quantum leaps". This process is called exciting an electron, and the higher energy levels are called "excited states" while the bottom level is called "grounded state". Thermionic work functionThe work function is also important in the theory of thermionic emission. Here the electron gains its energy from heat rather than photons. In this case, as for an electron escaping from the heated negatively-charged filament of a vacuum tube, the work function may be called the thermionic work function. Tungsten is a very common metal for vacuum tube elements, with a work function of approximately 4.5 eV. Thermionic emission requires a filament heating current (if), to maintain a temperature of 2000-2700 K. A saturation state of the filament current is reached, where a minor change in the filament current does not affect the beam current. The electron gun is then operated with the filament current very near the potential to overcome the work function (W)(Goldstein, 2003) The thermionic work function depends on the orientation of the crystal and will tend to be smaller for metals with an open lattice, larger for metals in which the atoms are closely packed. The range is about 1.5–6 eV. It is somewhat higher on dense crystal faces than open ones. ApplicationsIn electronics the work function is important for design of the metal-semiconductor junction in Schottky diodes and for design of vacuum tubes. MeasurementMany techniques have been developed based on different physical effects to measure the electronic work function of a sample. One may distinguish between two groups of experimental methods for work function measurements: absolute and relative. Methods of the first group employ electron emission from the sample induced by photon absorption (photoemission), by high temperature (thermionic emission), due to an electric field (field emission), or using electron tunnelling. All relative methods make use of the contact potential difference between the sample and a reference electrode. Experimentally, either an anode current of a diode is used or the displacement current between the sample and reference, created by an artificial change in the capacitance between the two, is measured (the Kelvin Probe method, Kelvin probe force microscope). Methods Based on PhotoemissionPhotoelectron emission spectroscopy (PES) is the general term for spectroscopic techniques based on the outer photoelectric effect. In the case of Ultraviolet Photoelectron Spectroscopy (UPS), the surface of a solid sample is irradiated with ultraviolet (UV) light and the kinetic energy of the emitted electrons is analysed. As UV light is electromagnetic radiation with an energy hν lower than 100 eV it is able to extract mainly valence electrons. Due to limitations of the escape depth of electrons in solids UPS is very surface sensitive, as the information depth is in the range of 2 – 20 monolayers (1-10nm). The resulting spectrum reflects the electronic structure of the sample providing information on the density of states, the occupation of states, and the work function. Methods Based on Thermionic EmissionThe retarding diode method is one of the simplest and oldest method of measuring work functions. It is based on the thermionic emission of electrons from an emitter. The current density J of the electrons collected by the sample depends on the work function φ of the sample and is given by the Richardson–Dushman equation J = AT2e − φ / kT where A, the Richardson constant, is a specific material constant. The current density increases rapidly with temperature and decreases exponentially with the work function. Changes of the work function can be easily determined by applying a retarding potential V between the sample and the electron emitter; φ is replaced by e(Φ + V) in above equation. The difference in the retarding potential measured at constant current is equivalent to the work function change, assuming that the work function and the temperature of the emitter is constant. One can use the Richardson–Dushman equation directly to determine the work function by temperature variation of the sample, as well. Rearranging the equation yields ln(J / T2) = ln(A) − φ / kT. The line produced by plotting ln(J / T2) vs. 1 / T will have a slope of − φ / k allowing to determine the work function of the sample. See also
ReferencesAs a book:
For a quick reference to values of work function of the elements:
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Work_function". A list of authors is available in Wikipedia. |





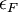 yet the two quantities are not exactly the same. This is due to the surface effect of a real-world solid: a real-world solid is not infinitely extended with electrons and ions repeatedly filling every
yet the two quantities are not exactly the same. This is due to the surface effect of a real-world solid: a real-world solid is not infinitely extended with electrons and ions repeatedly filling every 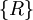 inside the geometrical region V which the solid occupies and then fill undistorted charge distribution basis into all primitive cells of
inside the geometrical region V which the solid occupies and then fill undistorted charge distribution basis into all primitive cells of 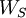 . And let
. And let 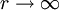 is zero. Then, the correct formula for work function is:
is zero. Then, the correct formula for work function is: