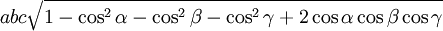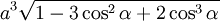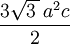My watch list

Bravais lattice

In geometry and crystallography, a Bravais lattice, named after Auguste Bravais, is an infinite set of points generated by a set of discrete translation operations. A crystal is made up of one or more atoms (the basis) which is repeated at each lattice point. The crystal then looks the same when viewed from any of the lattice points. In all, there are 14 possible Bravais lattices that fill three-dimensional space. Related to Bravais lattices are Crystallographic point groups of which there are 32 and Space groups of which there are 230.

Additional recommended knowledge

Don't let static charges disrupt your weighing accuracy

Correct Test Weight Handling Guide: 12 Practical Tips

How to ensure accurate weighing results every day?

Development of the Bravais lattices

The 14 Bravais lattices are arrived at by combining one of the seven crystal systems (or axial systems) with one of the lattice centerings. Each Bravais lattice refers a distinct lattice type.

The lattice centerings are:

Primitive centering (P): lattice points on the cell corners only
Body centered (I): one additional lattice point at the center of the cell
Face centered (F): one additional lattice point at center of each of the faces of the cell
Centered on a single face (A, B or C centering): one additional lattice point at the center of one of the cell faces.

Not all combinations of the crystal systems and lattice centerings are needed to describe the possible lattices. There are in total 7 × 6 = 42 combinations, but it can be shown that several of these are in fact equivalent to each other. For example, the monoclinic I lattice can be described by a monoclinic C lattice by different choice of crystal axes. Similarly, all A- or B-centered lattices can be described either by a C- or P-centering. This reduces the number of combinations to 14 conventional Bravais lattices, shown in the table below.

Crystal system	Bravais lattices
triclinic	P
triclinic
monoclinic	P	C
monoclinic
orthorhombic	P	C	I	F
orthorhombic
tetragonal	P	I
tetragonal
rhombohedral (trigonal)	P
rhombohedral (trigonal)
hexagonal	A
hexagonal
cubic	P	I	F
cubic

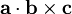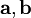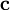The volume of the unit cell can be calculated by evaluating $\mathbf{a} \cdot \mathbf{b} \times \mathbf{c}$ where $\mathbf{a}, \mathbf{b}$ , and $\mathbf{c}$ are the lattice vectors. The volumes of the Bravais lattices are given below:

Crystal system	Volume
Triclinic	$abc \sqrt{1-\cos^2\alpha-\cos^2\beta-\cos^2\gamma+2\cos\alpha \cos\beta \cos\gamma}$
Monoclinic	$a b c sinα$
Orthorhombic	$a b c$
Tetragonal	$a 2 c$
Rhombohedral	$a^3 \sqrt{1 - 3\cos^2\alpha + 2\cos^3\alpha}$
Hexagonal	$\frac{3\sqrt{3\,}\, a^2c}{2}$
Cubic	$a 3$