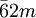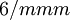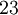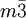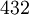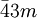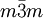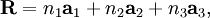To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Crystal systemA crystal system is a category of space groups, which characterize symmetry of structures in three dimensions with translational symmetry in three directions, having a discrete class of point groups. A major application is in crystallography, to categorize crystals, but by itself the topic is one of 3D Euclidean geometry. Product highlight
OverviewThere are 7 crystal systems:
There are 2, 13, 59, 68, 25, 27, and 36 space groups per crystal system, respectively, for a total of 230. The following table gives a brief characterization of the various crystal systems:
Within a crystal system there are two ways of categorizing space groups:
The 73 symmorphic space groups (see space group) are largely combinations, within each crystal system, of each applicable point group with each applicable Bravais lattice: there are 2, 6, 12, 14, 5, 7, and 15 combinations, respectively, together 61. Crystallographic point groupsA symmetry group consists of isometric affine transformations; each is given by an orthogonal matrix and a translation vector (which may be the zero vector). Space groups can be grouped by the matrices involved, i.e. ignoring the translation vectors (see also Euclidean group). This corresponds to discrete symmetry groups with a fixed point. There are infinitely many of these point groups in three dimensions. However, only part of these are compatible with translational symmetry: the crystallographic point groups. This is expressed in the crystallographic restriction theorem. (In spite of these names, this is a geometric limitation, not just a physical one.) The point group of a crystal, among other things, determines the symmetry of the crystal's optical properties. For instance, one knows whether it is birefringent, or whether it shows the Pockels effect, by simply knowing its point group. Overview of point groups by crystal system
The crystal structures of biological molecules (such as protein structures) can only occur in the 11 enantiomorphic point groups, as biological molecules are invariably chiral. The protein assemblies themselves may have symmetries other than those given above, because they are not intrinsically restricted by the Crystallographic restriction theorem. For example the Rad52 DNA binding protein has an 11-fold rotational symmetry (in human), however, it must form crystals in one of the 11 enantiomorphic point groups given above. Classification of lattices
Such symmetry groups consist of translations by vectors of the form where n1, n2, and n3 are integers and a1, a2, and a3 are three non-coplanar vectors, called primitive vectors. These lattices are classified by space group of the translation lattice itself; there are 14 Bravais lattices in three dimensions; each can apply in one crystal system only. They represent the maximum symmetry a structure with the translational symmetry concerned can have. All crystalline materials must, by definition fit in one of these arrangements (not including quasicrystals). For convenience a Bravais lattice is depicted by a unit cell which is a factor 1, 2, 3 or 4 larger than the primitive cell. Depending on the symmetry of a crystal or other pattern, the fundamental domain is again smaller, up to a factor 48. The Bravais lattices were studied by Moritz Ludwig Frankenheim (1801-1869), in 1842, who found that there were 15 Bravais lattices. This was corrected to 14 by A. Bravais in 1848. See also
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Crystal_system". A list of authors is available in Wikipedia. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||





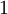
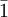
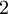
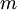
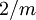
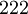
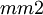
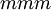
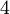
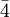
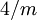
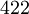
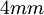
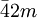 or
or 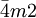
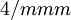
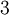
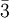
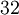 or
or 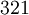 or
or 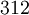
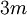 or
or 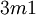 or
or 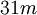
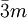 or
or 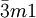 or
or 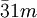
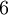
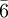
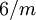
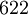
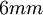
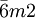 or
or