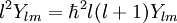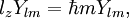To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Hydrogen-like atomA hydrogen-like atom is an atom with one electron. Except for the hydrogen atom itself (which is neutral) these atoms carry the positive charge e(Z-1), where Z is the atomic number of the atom. Because hydrogen-like atoms are two-particle systems with an interaction depending only on the distance between the two particles, their (non-relativistic) Schrödinger equation can be solved in analytic form. The solutions are one-electron functions and are referred to as hydrogen-like atomic orbitals.[1] Hydrogen-like atomic orbitals are eigenfunctions of the one-electron angular momentum operator l and its z component lz. The energy eigenvalues do not depend on the corresponding quantum numbers, but solely on the principal quantum number n. Hence, a hydrogen-like atomic orbital is uniquely identified by the values of: principal quantum number n, angular momentum quantum number l, and magnetic quantum number m. To this must be added the two-valued spin quantum number ms = ±½ in application of the Aufbau principle. This principle restricts the allowed values of the four quantum numbers in electron configurations of more-electron atoms. In hydrogen-like atoms all degenerate orbitals of fixed n and l, lz and s varying between certain values (see below) form an atomic shell. The Schrödinger equation of atoms or atomic ions with more than one electron cannot be solved analytically, because of the Coulomb interaction between the electrons. Numerical methods must be applied in order to obtain (approximate) wavefunctions or other properties from quantum mechanical calculations. Due to the spherical symmetry (of the Hamiltonian), the total angular momentum L of an atom is a conserved quantity. Many numerical procedures start from products of atomic orbitals that are eigenfunctions of the one-electron operators l and lz. The radial parts of these atomic orbitals are sometimes numerical tables or are sometimes Slater orbitals. By angular momentum coupling many-electron eigenfunctions of L2 (and possibly S2) are constructed. In quantum chemical calculations hydrogen-like atomic orbitals cannot serve as an expansion basis, because they are not complete. The non-square-integrable continuum (E > 0) states must be included to obtain a complete set, i.e., to span all of one-electron Hilbert space.[2] Product highlight
Mathematical characterizationThe atomic orbitals of hydrogen-like atoms are solutions to the Schrödinger equation in a spherically symmetric potential. In this case, the potential term is the potential given by Coulomb's law: where
After writing the wave function as a product of functions: (in spherical coordinates), where Ylm are spherical harmonics, we arrive at the following Schrödinger equation: where μ is, approximately, the mass of the electron. More accurately, it is the reduced mass of the system consisting of the electron and the nucleus. Different values of l give solutions with different angular momentum, where l (a non-negative integer) is the quantum number of the orbital angular momentum. The magnetic quantum number m (satisfying Non-relativistic Wave function and energyIn addition to l and m, a third integer n > 0, emerges from the boundary conditions placed on R. The functions R and Y that solve the equations above depend on the values of these integers, called quantum numbers. It is customary to subscript the wave functions with the values of the quantum numbers they depend on. The final expression for the normalized wave function is: where:
Relativistic Wave function and energyQuantum relativistic treatment of electrons uses Dirac equation. In this approach energy levels depends on n (principal quantum number) and m (magnetic quantum number)[3], energies allowed are: Where:
If we discount energy associated with rest mass of electron levels can be written as: Quantum numbersThe quantum numbers n, l and m are integers and can have the following values: See for a group theoretical interpretation of these quantum numbers this article. Among other things,
this article gives group theoretical reasons why Angular momentumEach atomic orbital is associated with an angular momentum l. It is a vector operator, and the eigenvalues of its square l2 ≡ lx2 + ly2 + lz2 are given by: The projection of this vector onto an arbitrary direction is quantized. If the arbitrary direction is called z, the quantization is given by: where m is restricted as described above. Note that l2 and lz commute and have a common eigenstate, which is in accordance with Heisenberg's uncertainty principle. Since lx and ly do not commute with lz, it is not possible to find a state which is an eigenstate of all three components simultaneously. Hence the values of the x and y components are not sharp, but are given by a probability function of finite width. The fact that the x and y components are not well-determined, implies that the direction of the angular momentum vector is not well determined either, although its component along the z-axis is sharp. These relations do not give the total angular momentum of the electron. For that, electron spin must be included. This quantization of angular momentum closely parallels that proposed by Niels Bohr (see Bohr model) in 1913, with no knowledge of wavefunctions. Including spin-orbit interaction
In a real atom the spin interacts with the magnetic field created by the electron movement around the nucleus, a phenomenon known as spin-orbit interaction. When one takes this into account, the spin and angular momentum are no longer conserved, which can be pictured by the electron precessing. Therefore one has to replace the quantum numbers l, m and the projection of the spin ms by quantum numbers which represent the total angular momentum (including spin), j and mj, as well as the quantum number of parity. Notes
See alsoReferences
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Hydrogen-like_atom". A list of authors is available in Wikipedia. |





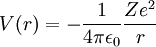
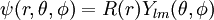
![\left[ - \frac{\hbar^2}{2\mu} \left({1 \over r^2}{\partial \over \partial r}\left(r^2 {\partial R(r)\over \partial r}\right) + {l(l+1)R\over r^2} \right) + V(r)R(r) \right]= E R(r),](images/math/2/7/c/27c2de2bedd0fc2996cf4fa67a123087.png)
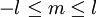 ) is the (quantized) projection of the orbital angular momentum on the z-axis. See here for the steps leading to the solution of this equation.
) is the (quantized) projection of the orbital angular momentum on the z-axis. See here for the steps leading to the solution of this equation.
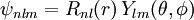
![R_{nl} (r) = \sqrt {{\left ( \frac{2 Z}{n a_{\mu}} \right ) }^3\frac{(n-l-1)!}{2n[(n+l)!]} } e^{- Z r / {n a_{\mu}}} \left ( \frac{2 Z r}{n a_{\mu}} \right )^{l} L_{n-l-1}^{2l+1} \left ( \frac{2 Z r}{n a_{\mu}} \right )](images/math/8/d/6/8d6fac13f8a7bbd9ad571ecf3a5f5992.png)
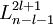 are the generalized Laguerre polynomials in the definition given here.
are the generalized Laguerre polynomials in the definition given here.
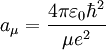
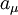 is approximately equal to
is approximately equal to 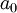 (the
(the 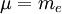 and
and 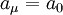 .
.
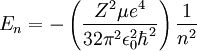 .
.
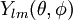 function is a
function is a 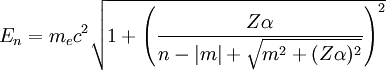
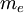 , is the mass of
, is the mass of 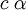 , are
, are 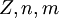 , are the number of protons of the nucleus, principal quantum number and magnetic quantum number.
, are the number of protons of the nucleus, principal quantum number and magnetic quantum number.
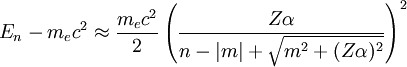
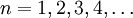
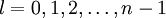
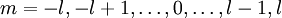
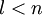 and
and 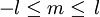 .
.