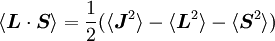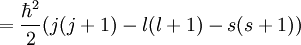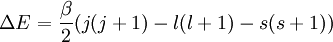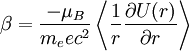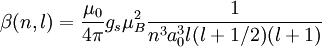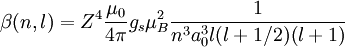To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Spin-orbit interaction
Product highlight
Spin-orbit interaction in atomic energy levelsIn this section, we will present a relatively simple and quantitative description of the spin-orbit interaction for an electron bound to an atom, using some semiclassical electrodynamics and non-relativistic quantum mechanics, up to first order in perturbation theory. This gives results that agree well, but not perfectly, with observations. A more rigorous derivation of the same result would start with the Dirac equation, and achieving a more precise result would involve calculating small corrections from quantum electrodynamics; both of these are presently beyond the scope of this article. Energy of a magnetic momentThe energy of a magnetic moment in a magnetic field is given by: where μ is the magnetic moment of the particle and B is the magnetic field it experiences. Magnetic fieldWe shall deal with the magnetic field first. Although in the rest frame of the nucleus, there is no magnetic field, there is one in the rest frame of the electron. Ignoring for now that this frame is not inertial, we end up with the equation where v is the velocity of the electron and E the electric field it travels through. Now we know that E is radial so we can rewrite Next, we express the electric field as the gradient of the electric potential where U = Ve is the potential energy of the electron in the central field, and e is the elementary charge. Now we remember from classical mechanics that the angular momentum of a particle It is important to note at this point that B is a positive number multiplied by L, meaning that the magnetic field is parallel to the orbital angular momentum of the particle. Magnetic Moment of the ElectronThe magnetic moment of the electron is where Interaction EnergyThe interaction energy is Let's substitute in the derived expressions. We have not, thus far, taken into account the non-inertiality of the electron rest frame; this effect is called Thomas precession and introduces a factor of Evaluating the energy shiftThanks to all the above approximations, we can now evaluate the energy shift exactly in this model. In particular, we wish to find a basis that diagonalizes both H0 (the non-perturbed Hamiltonian)and ΔH. To find out what basis this is, we first define the total angular momentum operator Taking the dot product of this with itself, we get (since L and S commute), and therefore It can be shown that the five operators H0, J², L², S², and Jz all commute with each other and with ΔH. Therefore, the basis we were looking for is the simultaneous eigenbasis of these five operators (i.e., the basis where all four are diagonal). Elements of this basis have the five quantum numbers n (the "principal quantum number") j (the "total angular momentum quantum number"), l (the "orbital angular momentum quantum number"), s (the "spin quantum number"), and jz (the "z-component of total angular momentum"). To evaluate the energies, we note that for hydrogenic wavefunctions (here Final Energy ShiftWe can now say where For hydrogen, we can write the explicit result For any singly-ionized atom which has Z proton
See alsoReferences
|
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Spin-orbit_interaction". A list of authors is available in Wikipedia. |





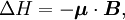
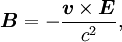
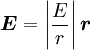 .
Also we know that the momentum of the electron
.
Also we know that the momentum of the electron 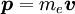 . Substituting this in and changing the order of the cross product gives:
. Substituting this in and changing the order of the cross product gives:
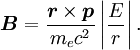
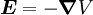 . Here we make the
. Here we make the 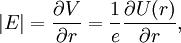
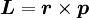 . Putting it all together we get
. Putting it all together we get
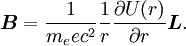
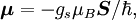
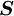 is the magnitude of its spin angular momentum,
is the magnitude of its spin angular momentum, 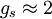 is the electron spin
is the electron spin 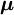 is a negative constant multiplied by the spin, so the
is a negative constant multiplied by the spin, so the 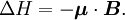
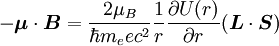
 . So
. So
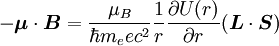
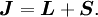
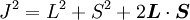
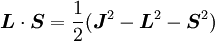
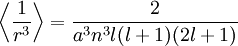
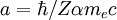 is the
is the