To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Darcy friction factor
The Darcy-Weisbach friction factor is a dimensionless number used in internal flow calculations with the Darcy-Weisbach equation. It expresses the linear relationship between mean flow velocity and pressure gradient. Product highlightIt is defined as: where:
The factor is named after French engineer Henry Darcy and German engineer Julies Weisbach. It may be evaluated for given conditions by the use of various empirical or theoretical correlations, or it may be obtained from published charts. These charts are often referred to as Moody diagrams, after L. F. Moody, and hence the factor itself is sometimes called the Moody friction factor. Also sometimes called a Blasius friction factor, after the approximate equation he proposed. The Darcy-Weisbach friction factor is 4 times larger than the Fanning friction factor, so attention must be paid to note which one of these is meant in the "friction factor" chart or equation consulted. Of the two, the Darcy-Weisbach factor is more commonly used by civil engineers, and the Fanning factor by chemical and mechanical engineers. Most importantly, however, is to use the correct friction factor that is corresponds to whatever table or chart you are using. (Most charts or tables indicate the type of friction factor, or at least provide the slope of the linear relation between the friction factor as a function of Reynolds number. If the slope is 16/Reynolds number, it's the Fanning factor, or if the slope is 64/Reynolds number, it's the Darcy-Weisbach factor.) References
Categories: Equations of fluid dynamics | Fluid dynamics |
||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Darcy_friction_factor". A list of authors is available in Wikipedia. |





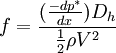
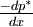 is the pressure drop per unit length
is the pressure drop per unit length


