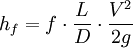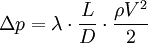Darcy-Weisbach equation

The Darcy-Weisbach equation is an important and widely used equation in hydraulics. It enables calculation of the head loss due to friction within a given length of pipe.

Additional recommended knowledge

Don't let static charges disrupt your weighing accuracy

How to quickly check pipettes?

What is the Sensitivity of my Balance?

The equation was initially a variant on the Prony equation; this variant was developed by Henry Darcy of France, and further refined into the form used today by Julius Weisbach of Saxony in 1845:

where the head loss due to friction h_f is a function of:

• a Darcy friction factor, f
• the ratio of the length to diameter of the pipe, L/D
• the velocity of the flow, V
• the standard constant for acceleration due to gravity g.

The equation can also be written in terms of pressure loss:

where the pressure loss due to friction Δp is a function of:

• the coefficient of laminar, or turbulent flow, λ
• the ratio of the length to diameter of the pipe, L/D
• the density of the fluid, ρ
• the velocity of the flow, V

The pressure loss equation can be derived from the head loss equation by multiplying each side by ρ and g. This will demonstrate that λ and f are equivalent.

The friction factor f varies according to the parameters of the pipe and the velocity of the flow, and is known to high accuracy within certain flow regimes. For laminar flows, λ is simply equal to 64/Re, the Reynolds Number. However, data on its variation with velocity was initially lacking, so this equation was outperformed at first by the empirical Prony equation in many cases. In later years it was eschewed in many special-case situations in favor of a variety of empirical equations, notably the Hazen-Williams equation, most of which were significantly easier to use in calculations. However, since the advent of the calculator, ease of calculation is no longer a major issue, and so the Darcy-Weisbach equation's generality has made it the preferred one.

Methods for finding the friction factor f are to use a diagram, such as the Moody chart, the Colebrook-White equation, or the Swamee-Jain equation. While the diagram and Colebrook-White equation are iterative solutions, the Swamee-Jain equation allows f to be found directly for full flow in a circular pipe.