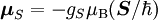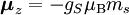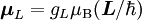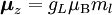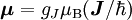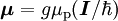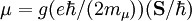My watch list

G-factor

Template:DISPLAYTITLE:g-factor

For the acceleration-related quantity in mechanics, see g-force.

A g-factor (also called g value or dimensionless magnetic moment) is a dimensionless quantity which characterizes the magnetic moment and gyromagnetic ratio of a particle or nucleus. It is essentially a proportionality constant that relates the observed magnetic moment μ of a particle to the appropriate angular momentum quantum number and the fundamental quantum unit of magnetism, the Bohr magneton.

Additional recommended knowledge

Correct Test Weight Handling Guide: 12 Practical Tips

How to quickly check pipettes?

Electron g-factors

There are three magnetic moments associated with an electron: One from its spin angular momentum, one from its orbital angular momentum, and one from its total angular momentum (the quantum-mechanical sum of those two components). Corresponding to these three moments are three different g-factors:

Electron spin g-factor

The most famous of these is the electron spin g-factor, g_S (more often called simply the electron g-factor, g_e), defined by

$\boldsymbol{\mu}_S=-g_S \mu_\mathrm{B} (\boldsymbol{S}/\hbar)$

where μ_S is the total magnetic moment resulting from the spin of an electron, S is the magnitude of its spin angular momentum, and μ_B is the Bohr magneton. The z-component of the magnetic moment then becomes

$\boldsymbol{\mu}_z=-g_S \mu_\mathrm{B} m_s$

The value g_S is roughly equal to two, and is known to extraordinary accuracy.^[1]^[2] The reason it is not precisely two is explained by quantum electrodynamics.^[3]

Electron orbital g-factor

Secondly, the electron orbital g-factor, g_L, is defined by

$\boldsymbol{\mu}_L=g_L \mu_\mathrm{B} (\boldsymbol{L}/\hbar)$

where μ_L is the total magnetic moment resulting from the orbital angular momentum of an electron, L is the magnitude of its orbital angular momentum, and μ_B is the Bohr magneton. The value of g_L is exactly equal to one, by a quantum-mechanical argument analogous to the derivation of the classical magnetogyric ratio. For an electron in an orbital with a magnetic quantum number m_l, the z-component of the orbital angular momentum is

$\boldsymbol{\mu}_z=g_L \mu_\mathrm{B} m_l$

which, since g_L = 1, is just μ_Bm_l

Landé g-factor

Thirdly, the Landé g-factor, g_J, is defined by

$\boldsymbol{\mu}=g_J \mu_\mathrm{B} (\boldsymbol{J}/\hbar)$

where μ is the total magnetic moment resulting from both spin and orbital angular momentum of an electron, J = L+S is its total angular momentum, and μ_B is the Bohr magneton. The value of g_J is related to g_L and g_S by a quantum-mechanical argument; see the article Landé g-factor.

Nucleon and Nucleus g-factors

Protons, neutrons, and many nuclei have spin and magnetic moments, and therefore associated g-factors. The formula conventionally used is

$\boldsymbol{\mu}=g \mu_\mathrm{p} (\boldsymbol{I}/\hbar)$

where μ is the magnetic moment resulting from the nuclear spin, I is the nuclear spin angular momentum, and μ_p is the nuclear magneton.

Muon g-factor

The muon, like the electron has a g-factor from its spin, given by the equation

$\mathbf{\mu}=g (e\hbar/(2m_\mu)) (\mathbf{S}/\hbar)$

where μ is the magnetic moment resulting from the muon’s spin, S is the spin angular momentum, and m_μ is the muon mass.

The muon g-factor can be affected by physics beyond the Standard Model, so has been measured very precisely, in particular at the Brookhaven National Laboratory. As of November 2006, the experimentally measured value is 2.0023318416 with an uncertainy of 0.0000000013, compared to the theoretical prediction of 2.0023318361 with an uncertainty of 0.0000000010^[4]. This is a difference of 3.4 standard deviations, suggesting beyond-the-Standard-Model physics may be having an effect.

Measured g-factor Values

Currently accepted NIST g-factor values[1]
Elementary Particle	g-factor	Uncertainty
Electron $g e$	2.002 319 304 3622	0.000 000 000 0015
Neutron $g n$	3.826 085 46	0.000 000 90
Proton $g p$	5.585 694 701	0.000 000 056
Muon $g μ$	2.002 331 8396	0.000 000 0012

It should be noted that the electron g-factor is one of the most precisely measured values in physics, with its uncertainty beginning at the twelfth decimal place.

Notes and references

^ See CERN courier article
^ B Odom, D Hanneke, B D'Urso and G Gabrielse (2006). "New measurement of the electron magnetic moment using a one-electron quantum cyclotron". Physical Review Letters 97 (3): 030801. doi:10.1103/PhysRevLett.97.030801.
^ S J Brodsky, V A Franke, J R Hiller, G McCartor, S A Paston and E V Prokhvatilov (2004). "A nonperturbative calculation of the electron's magnetic moment". Nuclear Physics B 703 (1-2): 333-362. doi:10.1016/j.nuclphysb.2004.10.027.
^ Hagiwara, K.; Martin, A. D. and Nomura, Daisuke and Teubner, T. (2006). "Improved predictions for g-2 of the muon and alpha(QED)(M(Z)**2)".