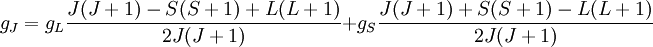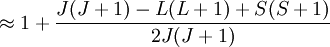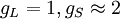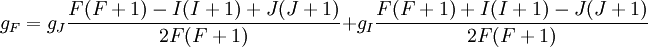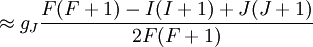Landé g-factor

In physics, the Landé g-factor is a particular example of a g-factor, namely for an electron with both spin and orbital angular momenta. It is named after Alfred Landé, who first described it in 1921.

Additional recommended knowledge

Recognize and detect the effects of electrostatic charges on your balance

Weighing the right way

Daily Sensitivity Test

In atomic physics, it is a multiplicative term appearing in the expression for the energy levels of an atom in a weak magnetic field. The quantum states of electrons in atomic orbitals are normally degenerate in energy, with the degenerate states all sharing the same angular momentum. When the atom is placed in a weak magnetic field, however, the degeneracy is lifted.

The factor comes about during the calculation of the first-order perturbation in the energy of an atom when a weak uniform magnetic field (that is, weak in comparison to the system's internal magnetic field) is applied to the system. Formally we can write the factor as,

Here, J is the total electronic angular momentum, L is the orbital angular momentum, and S is the spin angular momentum. Because S=1/2 for electrons, one often sees this formula written with 3/4 in place of S(S+1). The quantities g_L and g_S are other g-factors of an electron, as defined in the article on g-factors.

If we wish to know the g-factor for an atom with total atomic angular momentum F=I+J,

This last approximation is justified because g_I is smaller than g_J by the ratio of the electron mass to the proton mass.