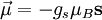To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Magnetic moment
In physics, astronomy, chemistry, and electrical engineering, the term magnetic moment of a system (such as a loop of electric current, a bar magnet, an electron, a molecule, or a planet) usually refers to its magnetic dipole moment, and is a measure of the strength of the system's net magnetic source. Specifically, magnetic dipole moment quantifies the contribution of the system's internal magnetism to the external dipolar magnetic field produced by the system (i.e. the component of the external magnetic field that drops off with distance as the inverse square). Any dipolar magnetic field pattern is symmetric with respect to rotations around a particular axis, therefore it is customary to describe the magnetic dipole moment that creates such a field as a vector with a direction along that axis. For quadrupolar, octupolar, and higher-order multipole magnetic moments, see Multipole expansion. Product highlightTwo kinds of magnetic sourcesFundamentally, contributions to any system's magnetic moment may come from sources of two kinds: (1) motion of electric charges, such as electric currents and (2) the intrinsic magnetism of elementary particles, such as the electron. Contributions due to the sources of the first kind can be calculated from knowing the distribution of all the electric currents (or, alternatively, of all the electric charges and their velocities) inside the system, by using the formulas below. On the other hand, the magnitude of each elementary particle's intrinsic magnetic moment is a fixed number, often measured experimentally to a great precision. For example, any electron's magnetic moment is measured to be −9.284764×10-24 J/T. The direction of the magnetic moment of any elementary particle is entirely determined by the direction of its spin (the minus in front of the value above indicates that any electron's magnetic moment is antiparallel to its spin). Finally, the net magnetic moment of any system is a vector sum of contributions from one or both types of sources. For example, a hydrogen atom's magnetic moment is a vector sum of the following contributions: the intrinsic moment of the electron, the orbital motion of the electron around the proton, and the intrinsic moment of the proton. Formulas and values for calculating magnetic momentsIn the simplest case of a planar loop of electric current, its magnetic moment is defined as: where
By convention, the direction of the vector area is given by the right hand rule (moving one's right hand in the direction of the current around the loop, when the palm of the hand is "touching" the loop's outer edge, and the straight thumb indicates the direction of the vector area and thus of the magnetic moment). In case of an arbitrary closed loop of constant current I, the magnetic moment is given by where In the most general case of an arbitrary current distribution in space, the magnetic moment of such a distribution can be found from the following equation: where
The above equation can be used for calculating a magnetic moment of any assembly of moving charges, such as a spinning charged solid, by substituting
For example, the magnetic moment produced by an electric charge moving along a circular path is
where For a free point charge moving in an external magnetic field the magnetic moment is a measure of the magnetic flux set up by the gyration of the charge in the magnetic field. The moment is opposite to the direction of magnetic field (i.e. it is diamagnetic) and is equal to the kinetic energy of the rotary motion divided by the magnetic field. For a spinning charged solid with a uniform charge density to mass density ratio, the ratio of its magnetic moment to its angular momentum, also known as gyromagnetic ratio, is equal to half the charge-to-mass ratio. This implies that a more massive assembly of charges spinning with the same angular momentum will have a proportionately weaker magnetic moment, compared to its lighter counterpart. Even though atomic particles cannot be accurately described as spinning charge distributions of uniform charge-to-mass ratio, this general trend can be sometimes observed in the atomic world, where intrinsic angular momenta of most particles are fairly constant: a small half-integer (spin) times the reduced Planck constant In atomic and nuclear physics, the symbol μ represents the magnitude of the magnetic moment, often measured in Bohr magnetons or nuclear magnetons, associated with the intrinsic spin of the particle and/or with the orbital motion of the particle in a system. Values of the intrinsic magnetic moments of some particles are given in the table below:
For relation between the notions of magnetic moment and magnetization see magnetization. Magnetic field produced by a magnetic momentAny system possessing a net magnetic dipole moment Chosing a frame of reference in which the system center is at the origin, and the z axis is pointing in the direction of the system's magnetic moment
Effects of an external magnetic field on a magnetic momentEquivalently, the magnetic moment of an object can be defined as a vector relating the aligning torque on the object from an externally applied magnetic field to the field vector itself. The relationship is given by where
A magnetic moment in an externally-produced magnetic field has a potential energy U: In a case when the external magnetic field is non-uniform, there will be a force, proportional to the magnetic field gradient, acting on the magnetic moment itself. Magnetic poles, analogy with the electric dipole momentMagnetic moment can be visualized as a bar magnet which has magnetic poles of equal magnitude but opposite polarity. Each pole is the source of magnetic force which weakens with distance. Since magnetic poles always come in pairs, their forces partially cancel each other because while one pole pulls, the other repels. This cancellation is greatest when the poles are close to each other i.e. when the bar magnet is short. The magnetic force produced by a bar magnet, at a given point in space, therefore depends on two factors: on both
the strength p of its poles, and on the distance d separating them. The force is proportional to the product Magnetic moment of electronsElectrons and many nuclei also have intrinsic magnetic moments, an explanation of which requires a quantum mechanical treatment and relates to the intrinsic angular momentum of the particles as discussed in the article electron magnetic dipole moment. It is these intrinsic magnetic moments that give rise to the macroscopic effects of magnetism, and other phenomena, such as nuclear magnetic resonance. The magnetic moment of the electron is where
and
Again it is important to notice that Magnetic moments of nuclei
The nuclear system is a complex physical system consisting of nucleons, i.e., protons and neutrons. The quantum mechanical properties of the nucleons include the spin among others. Since the electromagnetic moments of the nucleus depends on the spin of the individual nucleons, one can look at these properties with measurements of nuclear moments, and more specifically the nuclear magnetic dipole moment. The nuclear magnetic moment is very sensitive to the individual contributions from nucleons and a measurement or prediction of its value can reveal important information about the content of the nuclear wavefunction. There are several theoretical models that predict the value of the magnetic dipole moment and a number of experimental techniques aiming to carry out measurements in nuclei along the nuclear chart. Magnetic moments of moleculesAny molecule has a well-defined magnitude of magnetic moment, which may depend on the molecule's energy state. Typically, the overall magnetic moment of a molecule is a combination of the following contributions, in the order of their typical strength:
Examples of molecular magnetism
See alsoNotes
|
||||||||||||||||||||||||||||||||||||||||
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Magnetic_moment". A list of authors is available in Wikipedia. |





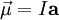
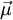 is the magnetic moment, a vector measured in
is the magnetic moment, a vector measured in 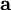 is the vector area of the current loop, measured in
is the vector area of the current loop, measured in 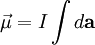
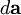 is the element of the vector area of the current loop.
is the element of the vector area of the current loop.
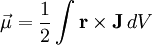
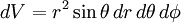 is the volume element,
is the volume element, 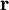 is the position vector pointing from the origin to the location of the volume element, and J is the current density vector at that location.
is the position vector pointing from the origin to the location of the volume element, and J is the current density vector at that location.
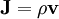 where
where 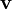 is the instantaneous linear velocity of that point.
is the instantaneous linear velocity of that point.
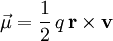 ,
,
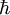 . This is the basis for defining the magnetic moment units of
. This is the basis for defining the magnetic moment units of 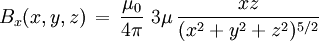
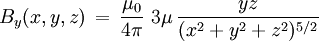
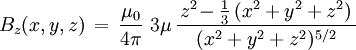 , as well as the 'transverse' component:
, as well as the 'transverse' component:
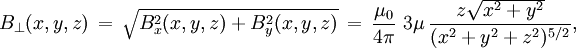
 is the torque, measured in newton-meters,
is the torque, measured in newton-meters,
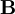 is the magnetic field, measured in teslas or, equivalently in newtons per (ampere-meter).
is the magnetic field, measured in teslas or, equivalently in newtons per (ampere-meter).
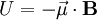
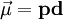 , where
, where