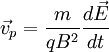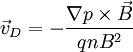To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
Guiding centerIn many cases of practical interest, the motion in a magnetic field of an electrically charged particle (such as an electron or ion in a plasma) can be treated as the superposition of a relatively fast circular motion around a point called the guiding center and a relatively slow drift of this point. The drift speeds may differ for various species depending on their charge states, masses, or temperatures, possibly resulting in electric currents or chemical separation. Product highlight
GyrationIf the magnetic field is uniform, the particle velocity is perpendicular to the field, and other forces and fields are absent, then the magnetic Lorentz force is perpendicular to both the velocity and the magnetic field and is constant in magnitude, resulting in particle motion at constant speed on a circular path. This is known as the gyration around the magnetic field. For mass m, charge q, and magnetic field B, the frequency of the circular motion, the gyro-frequency or cyclotron frequency, is For speed v, the radius of the orbit, called the gyroradius or Larmor radius, is Parallel motionSince the magnetic Lorentz force is always perpendicular to the magnetic field, it has no influence (to lowest order) on the parallel motion. In a uniform field with no additional forces, a charged particle will gyrate around the magnetic field according to the perpendicular component of its velocity and drift parallel to the field according to its initial parallel velocity, resulting in a helical orbit. If there is a force with a parallel component, the particle and its guiding center will be correspondingly accelerated. If the field has a parallel gradient, a particle with a finite Larmor radius will also experience a force in the direction away from the larger magnetic field. This effect is known as the magnetic mirror. While it is closely related to guiding center drifts in its physics and mathematics, it is nevertheless considered to be distinct from them. General force driftsGenerally speaking, when there is a force on the particles perpendicular to the magnetic field, then they drift in a direction perpendicular to both the force and the field. If
These drifts, in contrast to the mirror effect and the non-uniform B drifts, do not depend on finite Larmor radius, but are also present in cold plasmas. This may seem counterintuitive. If a particle is stationary when a force is turned on, where does the motion perpendicular to the force come from and why doesn't the force produce a motion parallel to itself? The answer is the interaction with the magnetic field. The force initially results in an acceleration parallel to itself, but the magnetic field deflects the resulting motion in the drift direction. Once the particle is moving in the drift direction, the magnetic field deflects it back against the external force, so that the average acceleration in the direction of the force is zero. There is, however, a one-time displacement in the direction of the force equal to (f/m)ωc-2, which should be considered a consequence of the polarization drift (see below) while the force is being turned on. The resulting motion is a cycloid. More generally, the superposition of a gyration and a uniform perpendicular drift is a trochoid. All drifts may be considered special cases of the force drift, although this is not always the most useful way to think about them. The obvious cases are electric and gravitational forces. The grad-B drift can be considered to result from the force on a magnetic dipole in a field gradient. The curvature, inertia, and polarisation drifts result from treating the acceleration of the particle as fictitious forces. The diamagnetic drift can be derived from the force due to a pressure gradient. Finally, other forces such as radiation pressure and collisions also result in drifts. Gravitational fieldA simple example of a force drift is a plasma in a gravitational field, e.g. the ionosphere. The drift velocity is Because of the mass dependence, the gravitational drift for the electrons can normally be ignored. The dependence on the charge of the particle implies that the drift direction is opposite for ions as for electrons, resulting in a current. In a fluid picture, it is this current crossed with the magnetic field that provides that force counteracting the applied force. Electric fieldThis drift, often called the Nonuniform EIf the electric field is not uniform, the above formula is modified to read Nonuniform BGuiding center drifts may also result not only from external forces but also from non-uniformities in the magnetic field. It is convenient to express these drifts in terms of the parallel and perpendicular energies In that case, the explicit mass dependence is eliminated. If the ions and electrons have similar temperatures, then they also have similar, though oppositely directed, drift velocities. Grad-B driftWhen a particle moves into a larger magnetic field, the curvature of its orbit becomes tighter, transforming the otherwise circular orbit into a cycloid. The drift velocity is Curvature driftIn order for a charged particle to follow a curved field line, it needs a drift velocity out of the plane of curvature to provide the necessary centripetal force. This velocity is Inertial driftA more general form of the curvature drift is the inertial drift, given by
where
In the important limit of stationary magnetic field and weak electric field, the inertial drift is dominated by the curvature drift term. Curved vacuum driftIn the limit of small plasma pressure, Maxwell's equations provide a relationship between gradient and curvature that allows the previous two drifts to be combined as follows For a species in thermal equilibrium, Polarization driftA time-varying electric field also results in a drift given by Obviously this drift is different from the others in that it cannot continue indefinitely. Normally an oscillatory electric field results in a polarization drift oscillating 90 degrees out of phase. Because of the mass dependence, this effect is also called the inertia drift. Normally the polarization drift can be neglected for electrons because of their relatively small mass. Diamagnetic driftThe diamagnetic drift is not actually a guiding center drift. A pressure gradient does not cause any single particle to drift. Nevertheless, the fluid velocity is defined by counting the particles moving through a reference area, and a pressure gradient results in more particles in one direction than in the other. The net velocity of the fluid is given by Drift CurrentsWith the important exception of the E-cross-B drift, the drift velocities of different species will be different. The differential velocity of charged particles results in a current, while the mass dependence of the drift velocity can result in chemical separation. ReferencesCosmic Plasma (1981), Hannes Alfvén |
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Guiding_center". A list of authors is available in Wikipedia. |





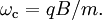
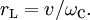
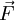 is the force on one particle, then the drift velocity is
is the force on one particle, then the drift velocity is
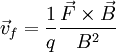 .
.
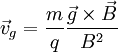
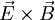 (E-cross-B) drift, is a special case because the force on the particles depends on their charge. As a result, ions (of whatever mass and charge) and electrons both move in the same direction at the same speed, so there is no net current (assuming
(E-cross-B) drift, is a special case because the force on the particles depends on their charge. As a result, ions (of whatever mass and charge) and electrons both move in the same direction at the same speed, so there is no net current (assuming 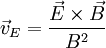
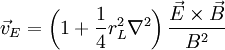
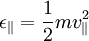
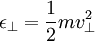
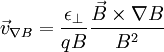
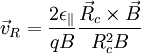
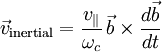 ,
,
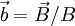 is the unit vector in the direction of the magnetic field. This drift can be decomposed into the sum of the curvature drift and the term
is the unit vector in the direction of the magnetic field. This drift can be decomposed into the sum of the curvature drift and the term
![\frac{v_\|}{\omega_c}\, \vec{b}\times\left[\frac{\partial\vec{b}}{\partial t} + (\vec{v}_E\cdot\nabla\vec{b}) \right]](images/math/9/2/7/9273cb8508093616a81ed044a218cd30.png) .
.
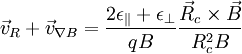
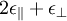 can be replaced by
can be replaced by 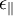 and
and 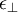 ).
).