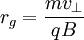To use all functions of this page, please activate cookies in your browser.
my.chemeurope.com
With an accout for my.chemeurope.com you can always see everything at a glance – and you can configure your own website and individual newsletter.
- My watch list
- My saved searches
- My saved topics
- My newsletter
GyroradiusThe gyroradius (also known as radius of gyration, Larmor radius or cyclotron radius) defines the radius of the circular motion of a charged particle in the presence of a uniform magnetic field. Product highlightwhere
Similarly, the frequency of this circular motion is known as the gyrofrequency or cyclotron frequency, and is given by: For electrons, this works out to be DerivationIf the charged particle is moving, then it will experience a Lorentz force given by: where Notice that the direction of the force is given by the cross product of the velocity and magnetic field. Thus, the Lorentz force will always act perpendicular to the direction of motion, causing the particle to move in a circle (gyrate). The radius of this circle rg can be determined by equating the magnitude of the Lorentz force to the centripetal force: where
Solving for rg, the gyroradius is determined to be: Thus, the gyroradius is directly proportional to the particle mass and velocity, and inversely proportional to the particle electric charge, and the magnetic field strength. See also
References & further reading
|
| This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Gyroradius". A list of authors is available in Wikipedia. |


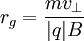



 is the gyroradius,
is the gyroradius,
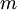 is the mass of the charged particle,
is the mass of the charged particle,
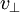 is the velocity component perpendicular to the direction of the magnetic field,
is the velocity component perpendicular to the direction of the magnetic field,
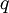 is the charge of the particle, and
is the charge of the particle, and
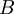 is the constant magnetic field.
is the constant magnetic field.
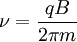
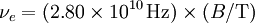
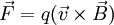
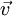 is the velocity vector,
is the velocity vector, 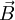 is the magnetic field vector, and
is the magnetic field vector, and 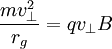
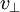 is the velocity component perpendicular to the direction of the magnetic field, and
is the velocity component perpendicular to the direction of the magnetic field, and